Article 2/25

Une manière de voir et de comprendre le mystère de l'arrangement géométrique qu'utilisent un grand nombre d'espèces végétales.

Beaucoup d'espèces végétales arrangent certains de leurs éléments dans une disposition très précise et esthétiquement merveilleuse :

Conifères : les écailles de leurs pives (helvétisme pour pomme de pin)
Tournesol : les graines dans le centre de la fleur
Cactus : leurs piquants
Ananas : leurs écailles
Artichauts : les touffes de foin implantées dans le coeur

La liste n'est pas exhaustive.

Comptage des spires

Spirale en construction

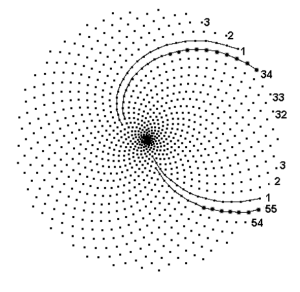
Cette disposition a un peu l'allure de la figure ci-dessus, formant deux ensembles de spires, l'un tournant dans le sens positif et l'autre dans les sens négatif.

Si l'on compte le nombre de spires dans un sens et dans l'autre (ici: 34 dans un sens et 55 dans l'autre), on constate avec une certaine stupéfaction qu'on tombe invariablement sur deux nombres consécutifs de la suite de Fibonacci: 1 1 2 3 5 8 13 21 34 55 89 144 ... et jamais sur d'autres nombres.

La suite de Fibonacci commence par deux 1 et chaque terme ultérieur est la somme des deux précédents.

Pourquoi en va-t-il ainsi ?

Il m'est apparu (après de nombreuses heures de contemplation méditative sur une pive) que ces espèces végétales procèdent de la manière suivante : elles implantent leurs écailles (ou feuilles ou graines) sur une spirale très lente en créant un objet tous les 137.50776°.

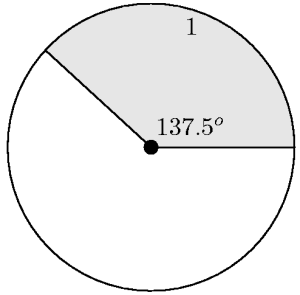
Ce nombre 137.50776 n'est pas n'importe quoi :

C'est l'angle correspondant à la division de la circonférence en deux parties proportionnelles à 1 et $\Phi$ où $\Phi = \mathrm{Phi} = \frac{1+\sqrt{5}}{2} = 1.618034\ldots$ est le fameux nombre d'or !

Dès lors apparaissent de manière automatique des spires très visibles en nombres égaux aux termes de la suite de Fibonacci, termes d'autant plus grands qu'on est plus loin du centre.

Une construction avec Cabri Géomètre (construction pouvant être téléchargée) permettra de se convaincre qu'il s'agit bien du nombre d'or exact et non pas de n'importe quel nombre voisin comme c'est le cas dans de nombreuses élucubrations d'ordre architectural ou pictural où le nombre d'or intervient comme une valeur mystique et sans aucune justification. 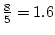Dans la plus grande partie de ces théories (sinon dans la totalité) on pourrait remplacer $\Phi$ par 1.6 sans aucun problème; simplement ça ferait moins sérieux, moins ésotérique... moins cosmique !

Ici pas du tout : 1.6 donne une localisation des éléments catastrophique. On constatera en faisant jouer la construction réalisée avec Cabri Géomètre qu'il faut, pour une bonne disposition, être exactement sur le nombre d'or.

On pourra rechercher cependant d'autres nombres favorables (pas aussi parfaits que le nombre d'or, mais presque). Par exemple

Angle $\alpha$	Rapport	Développement en fractions continues	Suite des réduites
137.5078°	1.61803 = $\frac{1+\sqrt{5}}{2}=\Phi$	1, 1, 1, 1, 1, 1, 1, 1, 1 $\ldots$	$\frac{1}{1}$ , $\frac{2}{1}$ , $\frac{3}{2}$ , $\frac{5}{3}$ , $\frac{8}{5}$ , $\frac{13}{8}$ , $\frac{21}{13}$ , $\frac{34}{21}$ , $\frac{55}{34}$ , $\frac{89}{55}\ldots$

149.1171°	1.41421 = $\sqrt{2}$	1, 2, 2, 2, 2, 2, 2, 2, 2 $\ldots$	$\frac{3}{2}$ , $\frac{7}{5}$ , $\frac{17}{12}$ , $\frac{41}{29}$ , $\frac{99}{70}$ , $\frac{239}{169}$ , $\frac{577}{408}\ldots$

163.1092°	1.20711 = $\frac{1+\sqrt{2}}{2}$	1, 4, 1, 4, 1, 4, 1, 4, 1 $\ldots$	$\frac{5}{4}$ , $\frac{6}{5}$ , $\frac{29}{24}$ , $\frac{35}{29}$ , $\frac{169}{140}$ , $\frac{204}{169}$ , $\frac{985}{816}\ldots$

151.1357°	1.38197 = $\frac{5-\sqrt{5}}{2}$	1, 2, 1, 1, 1, 1, 1, 1, 1 $\ldots$	$\frac{3}{2}$ , $\frac{4}{3}$ , $\frac{7}{5}$ , $\frac{11}{8}$ , $\frac{18}{13}$ , $\frac{29}{21}$ , $\frac{47}{34}$ , $\frac{76}{55}\ldots$

158.1447°	1.27639 = $1+\frac{\Phi}{3\Phi+1}$	1, 3, 1, 1, 1, 1, 1, 1, 1 $\ldots$	$\frac{4}{3}$ , $\frac{5}{4}$ , $\frac{9}{7}$ , $\frac{14}{11}$ , $\frac{23}{18}$ , $\frac{37}{29}$ , $\frac{60}{47}$ , $\frac{97}{76}\ldots$

Il s'agit d'une manière générale de réels dont le développement en fractions continues (voir encadré) est lent, c'est-à-dire où les termes successifs sont petits.

Le meilleur de tous ces nombres est $\Phi$ dont le développement est (1, 1, 1, 1...). C'est aussi (à ma connaissance) le seul nombre effectivement choisi par les végétaux. Les autres nombres conduisent à des nombres de spires différents des nombres de Fibonacci.

Les fractions réduites $(\frac{1}{1}$ , $\frac{2}{1}$ , $\frac{3}{2}$ , $\frac{5}{3}$ , $\frac{8}{5}$ , $\frac{13}{8}$ , $\frac{21}{13}$ , $\frac{\mathbf{34}}{21}$ , $\frac{\mathbf{55}}{34}\ldots)$ définies pour $\Phi$ par son développement en fractions continues définissent bien les nombres de spires. Mais on peut constater que ça ne fonctionne pas pour 1.38197 de développement 1, 2, 1, 1, 1... où les fractions réduites $(\frac{3}{2}$ , $\frac{4}{3}$ , $\frac{7}{5}$ , $\frac{11}{8}$ , $\frac{18}{13}$ , $\frac{29}{21}$ , $\frac{47}{34}\ldots)$ définissent les nombres 1, 3, 4, 7, 11, 18 ,29, 47, 76... (Suite dite de Lucas : même principe que Fibonacci mais commençant par 1, 3).

En faisant fonctionner la construction réalisée avec Cabri Géomètre, on rencontrera deux nombres de spires successifs 31 et 50 au lieu des 29 et 47 attendus. Il se trouve cependant que 31 et 50 sont la somme (numérateur + dénominateur) des fractions réduites $\frac{18}{13}$ et $\frac{29}{21}$ .

Ce même principe s'applique fort bien à la suite de Fibonacci. Il semble donc bien que:

Le nombre de spires est la somme numérateur + dénominateur

Donc, pour résumer, si une figure obtenue par la pose d'objets, tous les $\alpha$ degrés, sur une spirale, présente des spires dans deux sens alors le développement en fractions continues de $r=\frac{360^\mathrm{o}}{\alpha}-1$ est lent et les nombres de spires dans un sens et dans l'autre sont égaux à la somme du numérateur et du dénominateur de deux réduites successives du développement de .

Pour le nombre 1.27639, de développement 1, 3, 1, 1, 1, 1, 1..., l'angle $\alpha$ vaut 158.1451°, les réduites sont $\frac{4}{3}$ , $\frac{5}{4}$ , $\frac{9}{7}$ , $\frac{14}{11}$ , $\frac{23}{18}$ , $\frac{37}{29}$ , $\frac{60}{47}\ldots$ ce qui donne (numérateur + dénominateur) des nombres de spires successifs 7, 9, 16, 25, 41, 66... qu'on observe bien en faisant fonctionner le programme Cabri.

La construction réalisée avec Cabri Géomètre

On remarque que le nombre de spires (66) correspond bien à la somme numérateur + dénominateur d'un des termes de la suite des réduites $\frac{4}{3}$ , $\frac{5}{4}$ , $\frac{9}{7}$ , $\frac{14}{11}$ , $\frac{23}{18}$ , $\frac{37}{29}$ , $\frac{60}{47}\ldots$ définie à partir de = 1.27639...

Exemple d'une utilisation de la construction

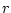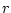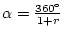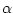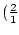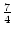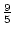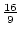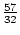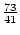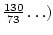Choisir un développement en fraction continue de termes successifs petits, par exemple (1, 1, 3, 1, 1, 3, 1, 1, 3,...) et calculer le nombre correspondant ( = 1.780776), l'angle $\alpha=\frac{360^\mathrm{o}}{1+r}$ ( $\alpha$ = 129.46°) ainsi que les premières fractions de la suite des réduites $(\frac{2}{1}$ , $\frac{7}{4}$ , $\frac{9}{5}$ , $\frac{16}{9}$ , $\frac{57}{32}$ , $\frac{73}{41}$ , $\frac{130}{73}\ldots)$ .
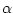Dans la construction créée avec Cabri Géomètre, déplacer les points verts situés sur les deux droites horizontales jusqu'à l'obtention du bon angle $\alpha$ .
À l'aide des traits noirs (dont on peut modifier le nombre, l'orientation et la longueur), compter les spires que présente la figure dans un sens puis dans l'autre (on obtient 89 dans un sens et 114 dans l'autre) et vérifier que ces nombres de spires correspondent bien à la somme numérateur + dénominateur de deux fractions de la suite des réduites...

Suite éventuelle dans un prochain numéro, en fonction de votre intérêt et de vos contributions sur la question.

Fractions continues

Tout nombre réel peut s'écrire sous la forme d'une fraction continue :

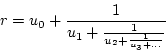
$\begin{displaymath} r = u_0 + \frac{1}{u_1+\frac{1}{u_2+\frac{1}{u_3+\ldots}}} \end{displaymath}$

On note $r=(u_0, u_1, u_2, u_3, \ldots)$ .

La suite $(u_0, u_1, u_2, u_3, \ldots)$ est le développement de $\alpha$ en fractions continues.

La suite des réduites , $r_1=u_0+\frac{1}{u_1}$ , $r_2=u_0+\frac{1}{u_1+\frac{1}{u_2}}$ , ... définie à partir du développement de en fractions continues convergent vers .

Fibonacci et nombre d'or en botanique

Exemple d'une utilisation de la construction

Fractions continues