Introduction

Chacun connaît les merveilleux "alicatados" de l'Alhambra de Grenade ou les mosaïques des mosquées un peu partout dans le monde. Les principes à la base de ces "pavages" sont par contre moins connus. Ils sont liés à quelques propriétés arithmétiques et géométriques élémentaires qui constituent autant de jolis problèmes mathématiques, certains simples d'autres plus compliqués.

Le sujet a été traité par de nombreux auteurs. Quelques fois l'approche est symbolique (voir Grabar, 1996, pour un exemple récent), mais la plpuart des études se situent à mi-chemin entre art plastique et mathématiques.

Un ouvrage précurseur est celui de Bourgoin (1879), "Eléments de l'art arabe, le trait des entrelacs", qui fournit une classification des patterns visibles dans des édifices du monde islamique. Les planches de l'ouvrage présentent un grand intérêt. Elles ont été réimprimées avec de brefs commentaires en anglais en 1973.

L'approche la plus connue est probablement celle liée aux groupes d'ornementation. Elle fait l'objet d'études classiques (Weyl, 1952, Coxeter, 1961) ou plus modernes (Abas & Salman, 1995, Hussein & Masayuki, 1999)^[1]. Toutefois, l'existence de patterns à base de figures à 10, voire 9 ou 7 côtés^[2] (fig 1) laisse penser que les recherches des mathématiciens arabes étaient d'un autre type, d'autant plus que plusieurs pavages "différents" peuvent correspondre à un même groupe d'ornementation^[3].

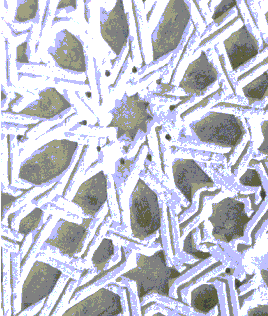
Figure 1: cette illustration tirée de Mülayim (1982) montre une rosace à 10 branches

Une autre approche paraît plus conforme à la philosophie originelle. Elle est principalement présentée dans des livres d'architecture. C'est celle que nous utiliserons. Selon cette approche, chaque ornement est construit à partir d'un recouvrement du plan par des polygones réguliers qui en représentent l'ordre sous-jacent souvent caché. La figure 2 montre un exemple de construction tiré de l'ouvrage de Critchlow (1976).

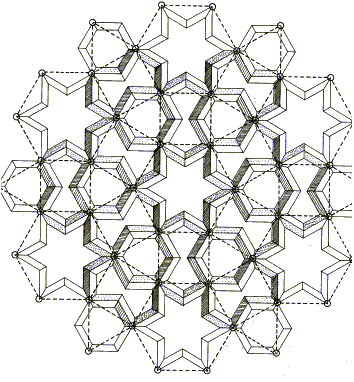
Figure 2: l'ornement est construit à partir du pavage en traitillés (auquel sera attribué ultérieurement le type N) en introduisant un "angle" sur chaque arête (reproduction tirée de Critchlow, 1976)

A noter que si un réseau de polygones réguliers est souvent utilisé comme base des ornements, ce n'est pas une règle générale. On trouve des exemples où les polygones ne sont pas tous réguliers (fig 3).

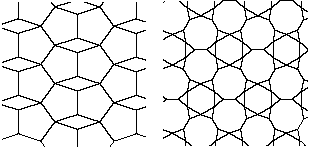
Figure 3: ces deux patterns sont repris de Kaplan. Le premier est bâti avec des losanges et des pentagones réguliers, les deux polygones ayant des cotés égaux. Le deuxième est construit avec des hexagones réguliers, des polygones réguliers à 9 côtés et des triangles isocèles (non équilatéraux)

Chaque pavage est caractérisé par ses sommets. A titre d'exemple, sur la figure 2, tous les sommets du pavage sous-jacent sont du même "type". Ils sont tous communs à un hexagone, un triangle et deux carrés.

Critchlow (1976) classe les pavages construits avec des polygones réguliers en trois familles, les réguliers, les semi-réguliers et les demi-réguliers. Ces familles seront décrites dans cet article à l'aide de méthodes « élémentaires ». Nous verrons également que la liste des pavages demi-réguliers semble incomplète et la conclusion fera quelques hypothèses à ce propos.

En cours de route, divers résultats sont énumérés dont chacun constitue une situation mathématique intéressante.

Un rappel

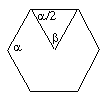
Résultat 1: la valeur de l'angle intérieur d'un polygone à n côtés vaut :

Avec les notations de la figure 4, on a la relation + = 180 .

Donc = 180 - . En amplifiant cette relation par n, nombre de côtés, on trouve que n (180 - ) = 360 d'où: n = 180n - 360 = 180 (n - 2) ce qui conduit au résultat recherché, élémentaire, mais qui ne manque pas d'élégance.

Figure 4: la mesure de l'angle intérieur d'un polygone est en relation avec la mesure de l'angle au centre

La famille des pavages réguliers

Ce sont ceux où un seul polygone est utilisé. Chaque sommet est donc entouré de 360/ polygones, c'est-à-dire: polygones.

Ce nombre doit être entier (positif) ce qui n'est possible que pour n = 3, 4, 6 ainsi que le montre facilement la transformation suivante:

Tous les sommets sont donc du même type. Ces pavages, ainsi que les sommets, seront respectivement désignés par les types (1), (2) et (3).

Résultat 2: il y a trois pavages réguliers. Ils sont représentés dans la figure 5.

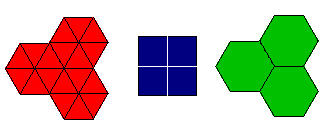
Figure 5: les trois pavages réguliers. Leur type est désigné par (1), (2), (3). Avec la notation (symbole) de Schläfli (1814-1895), ces pavages sont {3,6}, {4,4} et {6,3}

On remarquera le choix judicieux, pour ce travail de la découpe du tour complet en 360 parties^[4] !

Pour la suite, il est utile d'introduire la notion de "type" d'un sommet du pavage. Un sommet entouré de 3 polygones (d'ordre 3) ayant respectivement n₁, n₂ et n₃ côtés sera de type (n₁ , n₂ , n₃) (noté dans le sens contraire du mouvement des aiguilles d'une montre). Cette définition est prolongée aux sommets d'ordre quelconque dont deux exemples sont donnés dans la figure 6.

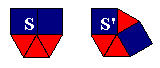
Figure 6: le sommet S est d'ordre 5 et de type (4, 4, 3, 3, 3) et le sommet S' est de type (4, 3, 3, 4, 3)

Les sommets des pavages réguliers de type (1), (2) et (3) sont respectivement de type (3, 3, 3, 3, 3, 3); (4, 4, 4, 4) et (6, 6, 6). Lorsqu'un pavage possède un sommet d'un seul type, il reçoit le type de ce sommet.

Les pavages semi-réguliers

Un pavage est semi-régulier si tous les sommets sont superposables par une isométrie, c'est-à-dire sont soit tous du même type, soit du même type à une symétrie près; par exemple: (4, 12, 6) et (4, 6, 12) sont superposables. Par contre, les sommets S et S' de la figure 6 ne le sont pas.

Résultat 3 : Chaque sommet doit être commun à moins 3 polygones et ce nombre ne peut pas excéder 6 (sinon l'un des polygones aurait un angle intérieur inférieur à 60°, ce qui est impossible pour un polygone régulier).

Les pavages semi-réguliers de sommets d'ordre 3

Ce sont les pavages où tous les sommets sont d'ordre 3 et du même type. Si ₁, ₂ et ₃ sont les angles intérieurs et n₁, n₂ et n₃ le nombre de côtés des polygones (fig 7), on a:

Résultat 4: la somme des inverses des nombres de côtés des polygones vaut 1/2.

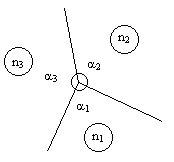
Figure 7: sommet d'ordre 3 de type (n₁, n₂, n₃)

La démonstration du résultat 4 se fait aisément à partir du résultat 1 .

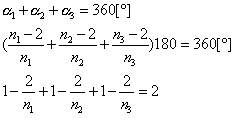
Trouver tous les triplets de nombre n₁, n₂ et n₃ dont la somme des inverses est la moitié de l'unité, voilà un premier petit problème concernant les nombres. Il est assez facile à résoudre par énumération dès que l'on a constaté que l'une des fractions doit être au moins égale à 1/6 et donc qu'un des dénominateurs (n₁ par exemple) est inférieur ou égal à 6 (et supérieur ou égal à 3).

Résultat 5 : Les solutions de la relation (II) sont données dans le tableau 1.

Tableau 1: triplets de nombres naturels dont la somme des inverses vaut 1/2

Solution no	n1	n2	n3	Type de sommet
1	3	7	42	A
2	3	8	24	B
3	3	9	18	C
4	3	10	15	D
5	3	12	12	E
6	4	5	20	F
7	4	6	12	G
8	4	8	8	H
9	5	5	10	I
10	6	6	6	3

Il est aisé de construire des sommets de chacun des types.

Par contre, ce n'est pas possible de construire un pavage semi-régulier pour tous ces types. On constate facilement que si un des n_i est impair alors les deux autres valeurs doivent être égales. En se référant à la figure 8, le sommet S' est de type (3, n_2, x) et S'' de type (3, x, n₁). Ils sont du même type que S qui est de type (3, n₁, n₂). Donc x = n₁= n₂.

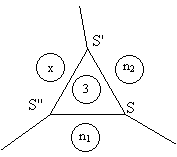
Figure 8: les "alentours" d'un polygone à nombre impair de côtés (triangle) dans un pavage semi-régulier d'ordre 3

Les solutions: 1, 2, 3, 4, 6 et 9 ne peuvent donc pas constituer des types de sommets d'un pavage semi-régulier. Il reste donc les solutions 5, 7, 8 (la solution 10 a déjà été vue précédemment) qui conduisent aux sommets et aux pavages de type E, G et H (figure 9).

Résultat 6: il y a 3 types de pavages semi-réguliers d'ordre 3. Ils correspondent aux sommets de types E, G, H.

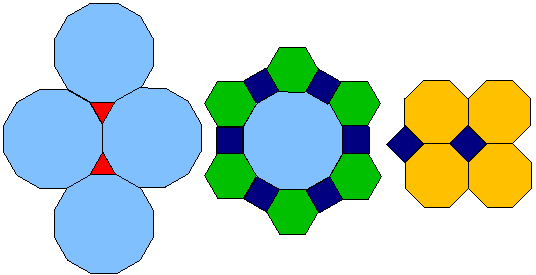
Figure 9: les pavages semi-réguliers d'ordre 3 de type E, G, H

Remarques:

1) L'hexagone peut être pavé par 6 triangles. Le dodécagone peut être pavé par un hexagone, 6 carrés et 6 triangles (fig 10) ou par 6 carrés et 12 triangles. Les pavages contenant des hexagones et des dodécagones peuvent donc être subdivisés.

2) Etant donnés des polygones, la construction du pavage correspondant se fait relativement facilement, les possiblités se révèlent rapidement en nombre limité. Malheureusement, les pièces de jeux de mosaïque trouvés sur le marché ne proposent pas les pièces utilisées ici (la plupart du temps, ces pièces sont construites sur la base du triangle isocèle rectangle).

Figure 10: décomposition du dodécagone en triangles, carrés et hexagone

Résultat 7: Pour les sommets d'ordre 4, 5 et 6 on a les relations suivantes:

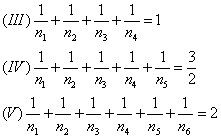
Elles s'obtiennent de manière identique au résultat 4:

Les pavages semi-réguliers de sommets d'ordre 4

Résultat 8: La relation (III) admet 4 solutions (à des permutations près). Elles sont données dans le tableau 2.

Tableau 2: quadruplet de nombres naturels dont la somme des inverses vaut 1

Solution	n1	n2	n3	n4	Type de sommet
1	3	3	4	12	L et L'
2	3	3	6	6	M et M'
3	3	4	4	6	N et N'
4	4	4	4	4	2

A noter que les trois premières solutions permettent chacune de construire deux types de sommets différents:

L = (3, 4, 3, 12); L' = (3, 3, 4, 12)
M = (3, 6, 3, 6) ; M' = (3, 3, 6, 6)
N = (3, 4, 6, 4); N' = (3, 4, 4, 6)

Il n'est pas possible de construire des pavages de type L, L', M', N' (selon un raisonnement semblable à celui conduisant au résultat 6). Mais on verra que des pavages peuvent être construits qui intègrent plusieurs de ces types.

Par contre, il est possible de construire des pavages de type M et N (fig 11) de façon unique. La solution 4 correspond au pavage régulier d'ordre 4 (type 2).

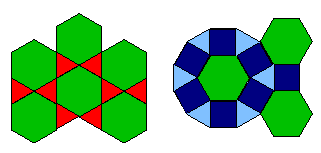
Figure 11: pavages semi-réguliers de types M et N

Les pavages semi-réguliers de sommets d'ordre 5

Résultat 9 : La relation (IV) admet 2 solutions (à des permutations près). Elles sont données dans le tableau 5.

Tableau 5: quintuplets de nombres naturels dont la somme des inverses vaut 3/2

Solution	n1	n2	n3	n4	n5	Type de sommet
1	3	3	3	4	4	Q et Q'
2	3	3	3	3	6	R

Q est le sommet de type: (3, 3, 4, 3, 4) et Q' de type (3, 3, 3, 4, 4)

La figure 12 montre que des patterns de type Q, Q' et R existent. Ils sont uniques.

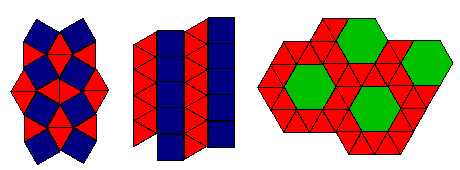
Figure 12: les pavages de types Q, Q', R

Les pavages semi-réguliers de sommets d'ordre 6

Résultat 10 : La relation (V) n'admet qu'une seule solution. Elle correspond au pavage triangulaire (type 1).

Résultat 11 : En définitive, il existe 3 pavages réguliers et 8 semi-réguliers.

Les pavages n-réguliers

Les pavages n-réguliers possèdent des sommets de n types différents (on propose de nommer 1-réguliers les pavages semi-réguliers et 0-réguliers les réguliers). L'ensemble des pavages n-réguliers (n>1) sont dits demi-réguliers.

On constate que les solutions d'ordre 3 qui n'ont pas permis de créer des pavages 1-réguliers, ne peuvent pas non plus être utilisées dans des pavages n-réguliers (n>1). En effet, dans chaque cas apparaît un couple unique de polygones qui n'apparaît dans aucun autre sommet. Par exemple, le sommet de type (3, 10, 15) devrait être relié à un sommet de type (3, 10, ...) qui n'existe pas.

Par conséquent les sommets des pavages demi-réguliers (n-réguliers avec n>1) ne peuvent être que d'un type déjà considéré : 1, 2, 3, E, G, H, M,N, Q, Q', R, auxquels il faut ajouter les sommets pour lesquels il n'existent pas de pavage semi-régulier: M', N', L et L'. On verra que tous pourront apparaître dans des pavages demi-réguliers (un exemple est donné par la figure 13). La figure 14 rassemble ces différents types de sommets.

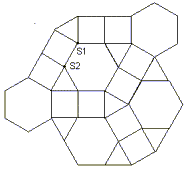
Figure 13: un pavage 2-régulier de type N+N' (S1 est de type N, S2 de type N'). Il existe un pavage 1-régulier de type N, mais il n'en existe pas de type N'

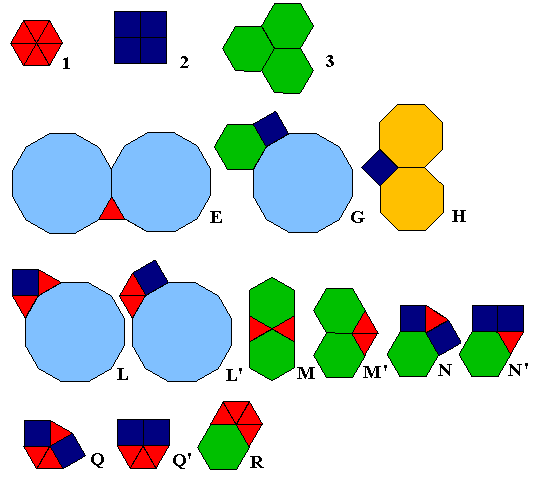
Figure 14: l'ensemble des sommets pouvant intervenir dans la construction de pavages n-réguliers

Vers un catalogue des pavages n-réguliers

Critchlow mentionne 14 pavages n-réguliers (n>1).

Il s'agit des pavages suivants^[5]:

2-réguliers: E+L ; L'+(1) ; M+G ; M+M' ; N+Q ; Q + (1) (2 constructions possibles)^[6] ; N+N' ; N+Q'

3-réguliers: L+L'+Q ; L'+Q+(1) ; N+Q'+Q ; Q'+Q+(1) (2 constructions possibles) ;

Etant donné une liste de sommets (par exemple N et Q), il est assez facile de construire tous les pavages les intégrant. Il est aussi aisé de voir, cas par cas, que d'autres constructions sont impossibles; par exemple: N'+Q' ; L+L', etc.

Par contre, le problème de l'exhaustivité générale demeure. Beaucoup d'autres pavages en plus de ceux dont Critchlow fait la liste peuvent être imaginés. Si certaines solutions, trop "simplistes", par exemple les pavages des figures 15 et 16, peuvent facilement être " éliminées " en évoquant des règles de subdivision homogène, d'autres constructions sont moins triviales comme celles proposées dans la figure 17.

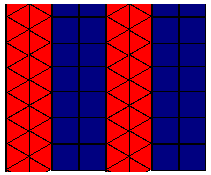
Figure 15: un pavage simple ne satisfaisant pas la règle d'iso-granularité. Le pavage possède des triangles constitués de 4 petits triangles

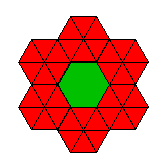
Figure 16: un pavage (de type R+1) ne respectant pas la règle d'iso-subdivision. Des hexagones sont d'une seule pièce, d'autres sont décomposés en 6 triangles

 

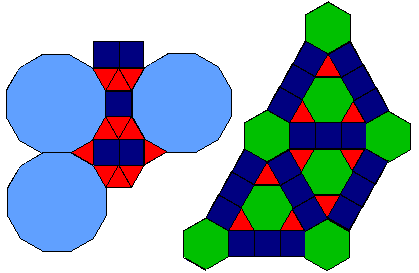
Figure 17: deux pavage ne faisant pas partie des 14 solutions classiques, celui de gauche est 4-réguliers, il est de type: E+L+L'+Q'. Celui de droite fournit une autre disposition que celle proposée dans la figure 13 pour un pavage de type N+N'

Pour conclure

Cet article a proposé une approche élémentaire de la construction des pavages liés aux ornements de l'art islamique. Il a permis d'évoquer des questions qui peuvent faire l'objet de situations mathématiques intéressantes.

Un certain nombre de questions certaines faciles d'autres qui paraissent plus ouvertes demeurent. Par exemple :

1) Le nombre de 14 pavages demi-réguliers avancé par Critchlow n'a pas pu être reproduit ni trouvé dans d'autres sources. Existe-t-il un critère de sélection permettant de caractériser exactement ces 14 pavages demi-réguliers ?

2) De façon plus générale, peut-on trouver une méthode permettant de faire la liste de tous les pavages n-réguliers (sans régles restrictives) ? (hypothèse: leur nombre est important).

3) Existe-t-il des pavages n-réguliers et non périodiques (non invariants par translation)? C'est une question facile à résoudre qui devrait permettre au lecteur d'entrer dans ce monde merveilleux des pavages du plan.

Bibliographie

Abas, S. J. & Salman, A. S. (1995). Symmetries of islamic geometrical patterns. World scientific.

Bourgoin, J. (1973) . Arabic Geometrical Pattern and Design. Reprint. Dover, New York.

Coxeter, H.S.M. (1961). Introduction to Geometry. New York: John Wiley & Sons.

Critchlow, K. (1976). Islamic Patterns. Reprint. London: Thames & Hudson.

Grabar, O. (1996). L'ornement: formes et fonctions dans l'art islamique. Paris: Flammarion.

Hussein, K. & Masayuki, N. (1999). Islamic Symmetric Pattern Generation based on Group Theory. Computer Graphics International, 1999, 112-119.

Mülayim, S. (1982). Anadolu türk mimarisinde, geometrik süslemeler. Kültür ve turizm bakanligi yayinlari.

Kaplan, C.S. (s.d). Computer generated islamic star patterns. Seattle: University of Washington, Departement of computer science and engineering. (urls: www.cs.washington.edu/homes/csk/taprats ,
members.tripod.com/vismath4/kaplan/index.htm)

Weyl, H. (1952). Symmetry. Princeton: University Press.