Introduction

Cet article présente une recherche en mathématique, réalisée au collège des Forges de l'école secondaire de la Chaux-de-Fonds, par deux étudiants de 9^ème année (15 ans) de la section « Maturité » pour leur travail d'option spécifique en « atelier de sciences ». Il s'agit de Céline Stähli et Yann Abbet qui se sont littéralement immergés dans leur sujet et qui ont été la plupart du temps autonomes dans leurs déductions et leurs découvertes, ainsi que pour leurs productions informatisées qu'ils ont effectuées à domicile.

La démarche de travail que je leur ai proposée est donnée par quatre situations mathématiques réparties sur 10 périodes:

1) Itération d'une fonction (2 périodes)
Familiarisation avec le concept d'itération

2) Itération d'une fonction linéaire (2 périodes)
Familiarisation avec la notion de convergence et divergence
Découverte d'une stratégie géométrique

3) Itération d'une fonction du 2^ème degré (2 périodes)
Familiarisation avec le concept d'attracteur
Recherche algébrique et géométrique

4) Convergence vers le chaos (4 périodes)
Quête et émergence du chaos
Découverte de l'augmentation du nombre de solutions de convergence

L'intérêt pédagogique de cet atelier porte sur différents niveaux :

1) J'ai proposé à mes élèves ce sujet d'étude sur le chaos, car je suis personnellement un passionné de la nouvelle géométrie fractale, ce qui m'a inévitablement conduit à m'intéresser aux systèmes chaotiques.

La relation maître – étudiants qui se construit, alors que les deux parties travaillent sur le même projet de recherche, est de haute qualité, associant motivations, échanges, plaisirs, et une reconnaissance réciproque.

2) L'itération d'une fonction est une approche particulièrement intéressante car elle sort de la perspective habituelle d'étude d'une fonction. C'est une approche relativiste, de « l'intérieur », de la même manière qu'Einstein a étudié la vitesse de la lumière en se plaçant « assis » sur un photon, image utilisée par lui-même et inspirée d'un de ses rêve d'enfance, pour illustrer le « référentiel mobile ».

Avec une itération, on se place « assis »sur la valeur de départ x , et on suit la trajectoire de la valeur au travers de la fonction y . On observe le comportement de la fonction, divergent ou convergent.

Cette perspective relativiste de « l'intérieur », donne une présentation de « ce que la fonction a dans le ventre ». De la même manière que l'on « scanne » les nombres naturels avec la décomposition en facteurs premiers, afin de savoir « ce que le nombre a dans le ventre », comme me l'a transmis mon maître de stage François Jaquet , lors de ma formation.

3) C'est B. Mandelbrot qui souligne le caractère « non linéaire » des systèmes chaotiques.

Cette «non-linéarité» est un objectif fondamental de l'enseignement des mathématiques au niveau secondaire. C'est par rapport à la « non-linéarité » que peut s'individualiser le concept particulier de « linéarité » (voir à ce sujet l'article de F. Jaquet , La tentation de la proportionnalité, Math-école 198, p.30).

4) Il faut enseigner le chaos. Quelle que soit la perfection atteinte par la mathématique linéaire, elle abuse inévitablement l'étudiant et fausse son jugement sur le monde, terriblement non-linéaire, qui ne possède pas nécessairement des propriétés dynamiques simples, mais complexes.

Cela devrait aussi être présent à l'esprit de nos dirigents. L'économie au travers de la bourse, l'écologie au travers du climat, la politique au travers du social, sont tous des systèmes chaotiques, susceptibles de basculer suite à « la goutte qui fait déborder le vase », ne suivant plus du tout une logique linéaire, mais au contraire une logique chaotique et complexe : crises monétaires, catastrophes écologiques ou guerres sociales.

Etre conscient de la fragilité et de la sensibilité des systèmes chaotiques, ouvre des perspectives nouvelles pour le développement durable de notre planète.

Plan de l'article

Les quatre situations seront présentées, l'une après l'autre avec chaque fois l'énoncé du problème suivi d'extrait des travaux réalisés par les élèves, le tout suivi d'un bref commentaire. Un bref complément théorique termine l'article.

Situation 1 : Itération d'une fonction

Problème Je dépose un capital de 100.- Frs dans une banque . Cette banque m'offre le 10% de mon capital après une année de dépôt de mon argent. Je laisse l'ensemble de mon argent à la banque, sans y toucher, durant plusieurs années. (ITERATION) a) Etudie en terme de fonctions la transformation du capital, année après année. b) Réalise un graphe sur papier millimétré. (projet pour la réalisation du graphe à l'ordinateur) Travail à l'ordinateur A l'aide d'un « éditeur graphique », tu peux représenter ta fonction mathématique. Imprime la formule mathématique ainsi que ton graphique, à différentes échelles, sur une feuille blanche tirée du logiciel « Word ». Recherche En utilisant ton graphique imprimé, essaye de découvrir une stratégie géométrique pour illustrer le processus d'itération. Afin de découvrir ce processus, construis et observe le tableau de valeurs représentant la fonction de la situation problème. Note la particularité de ce tableau, cela te permettra de définir ce qu'est une itération. (Tu utiliseras cette stratégie géométrique pour la suite de tes découvertes ...)

Travail réalisé

Commentaire

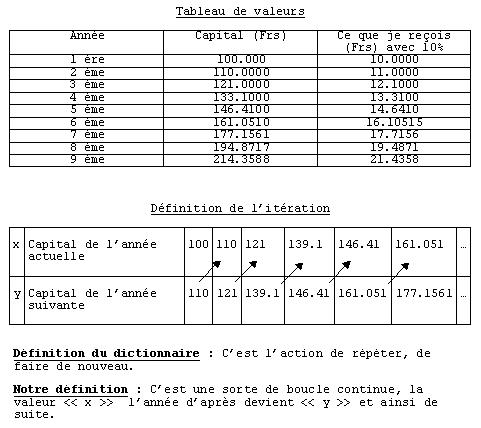
La figure montre la stratégie géométrique utilisée correspondant au calcul de l'itération, on prend une valeur de départ, ici x = 20, on cherche (ou calcule) la valeur de y correspondante (y = 22), on la reporte sur l'axe des x par symétrie (prend cette valeur comme nouvelle x) et on recommence.

A ne pas confondre, cette étude de la convergence et celle qui consisterait, par exemple, à l'étude du comportement asymptotique de la fonction.

Les élèves ont étudié ce comportement pour plusieurs valeurs initiales.

Situation 2 : Itération d'une fonction linéaire : Convergence et divergence

Observation du comportement d'une fonction itérée Définition Convergence : On dit que « y » converge si la valeur de « y » tend vers un nombre précis et fixe durant l'itération. Divergence : On dit que « y » diverge si la valeur de « y » tend vers l'infini durant l'itération. Problème Itérer des fonctions linéaires du type y = a x et indiquer pour quelle(s) valeur(s) de a « y » diverge ou converge. Pour cela complète un tableau de valeurs pour chaque fonction étudiée, ainsi que des représentations graphiques réalisées à l'ordinateur. Puis utilise la stratégie géométrique que tu as découverte pour voir si ces fonctions convergent ou divergent. A partir de tes observations, essaye de formuler une loi concernant l'itération des fonctions linéaires. Avec le logiciel Excel, programme la fonction y = a x sur une feuille de calcul, de manière à ce que si l'on donne une valeur à «  a  » et à «  x  », alors le programme nous fourni la valeur de « y ». Puis essaye de trouver un procédé de programmation simple pour itérer cette fonction.

Travail réalisé

Commentaire

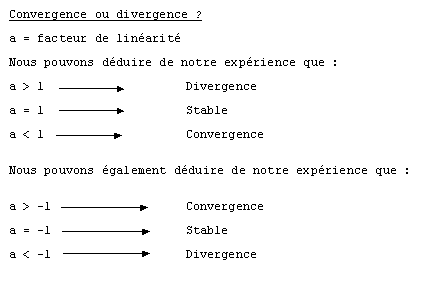
Un problème de nomenclature et de notation se pose. Il faudrait introduire les itérés de x par x_n+1 = f(x_n) ce qui paraît ajouter un formalisme difficile à maîtriser. La définition a été mise au point par discussion et on a parlé de convergence et de divergence de « y ».

Ici un échantillon des travaux sont présentés selon les deux méthodes : représentation sur la « carte du premier retour » et relation de la valeur de x en fonction de n, ceci pour diverses valeurs de la constante a . Pour ces deuxièmes représentations on notera que les ressources d'Excel sont utilisées pour le calcul et à partir des résultats la création du graphe (voir aussi ci-dessous).

La cas -1 pose problème puisqu'il y a à la fois non divergence et non convergence. La notion de stabilité a été introduite à cette fin !

Situation 3 : Itération d'une fonction du 2ème degré et attracteur

Problème Itérer de nombreuses fois une fonction simple. La fonction prend un nombre à l'entrée, et en rend un autre à la sortie, puis ce nombre sortant est réintroduit dans la fonction qui va en fournir un nouveau , etc. Exemples a) Fonction linéaire: y = 1,1 x (Evolution d'un capital financier année après année) Dans une banque, cette fonction exprime la relation entre le capital de cette année « x », et le capital de l'année prochaine « y ». 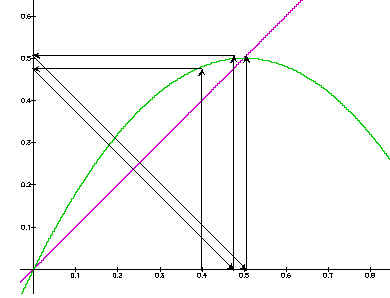b) Fonction du 2ème degré: y = a x - ax2 (Evolution d'une population animale année après année) Pour une population animale, cette fonction exprime la relation entre le nombre d'individus de cette année « x » et le nombre d'individus de l'année prochaine « y ». Tâche Réalise la représentation graphique de la fonction y = ax - ax2 pour la valeur a = 2,7 à l'aide de l'éditeur graphique et copie la formule et la représentation graphique sur une page blanche du logiciel Word que tu imprimeras à différentes échelles. Puis, grâce à la « stratégie géométrique » que tu as mis au point précédemment, essaye de déterminer si l'itération de cette fonction converge ou diverge. S'il y a convergence, détermine géométriquement (avec l'éditeur graphique) puis algébriquement (par résolution de l'équation) la valeur (x;y) du point de convergence. Ce point (x;y) vers lequel l'itération converge est appelé un attracteur.

Travail réalisé

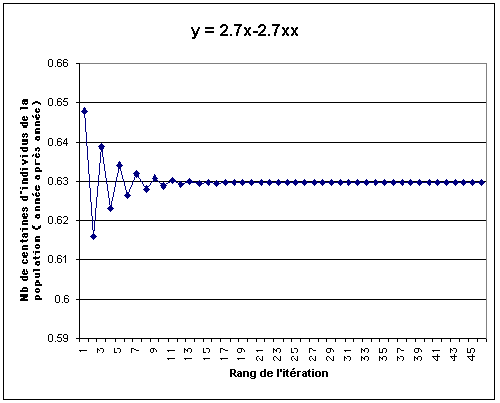
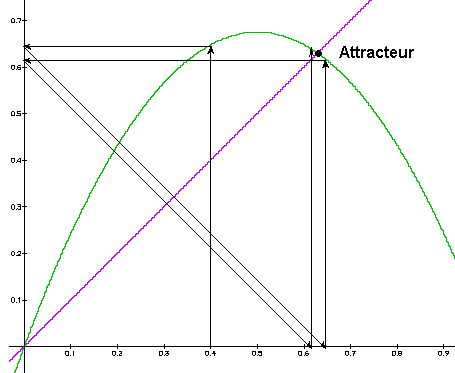
Commentaire

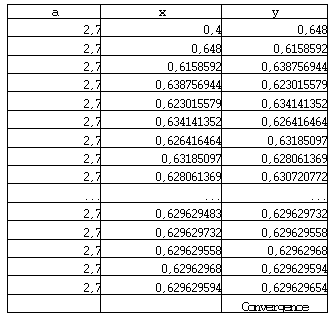
Cette activité est intermédiaire, on y retrouve les caractéristiques du cas linéaire et amorce le cas de l'équation logistique. On a représenté une partie de la feuille Excel qui permet d'obtenir les valeurs de l'inération et de dessiner le graphe de x en fonction du nombre d'itérations.

Situation 4: Convergence vers le chaos

Problème Etudier l'évolution d'une population animale, en terme de croissance ou diminution du nombre d'individus. (Exemple: oeufs-larves-papillons, cycle de reproduction d'une année, nourriture: feuilles et fleurs d'arbres). Avec une fonction linéaire, on aurait une population à croissance continue et illimitée, ce qui serait une aberration écologique, puisque cette population disparaîtrait en épuisant la nourriture de son environnement. L'évolution d'une population animale est plutôt une fonction du 2ème degré du type suivant: y = a x - a x2 Cette fonction est plus réaliste, car elle a la forme d'une « bosse » faisant chuter la population lorsqu'elle devient trop importante, ce qui correspond cette fois à une réalité écologique. En effet, la diminution de nourriture dûe à l'augmentation de la population, entraine une diminution de la reproduction de cette population pour l'année suivante. L'évolution de la population dépend de manière sensible de la valeur de a . Tâche Réalise une recherche mathématique détaillée, sur les différentes situations déterminées par la valeur de a . A chaque fois tu noteras la formule, la représentation graphique et l'attracteur (avec l'éditeur graphique sur une page blanche du logiciel Word). Avec un ordinateur et à l'aide du logiciel Excel, programme cette fonction y = a x - a x2 sur une feuille de calcul, de manière à ce que si l'on donne une valeur à « a » et à « x » alors le programme nous fourni la valeur de « y ». Puis à l'aide de ta page de calcul programmée sur Excel , tu imprimeras la représentation graphique de la convergence ou de la divergence de la fonction itérée. Enfin, tu essayeras d'interpréter en terme de biologie chacune des situations présentées.

Travail réalisé

a = 0.5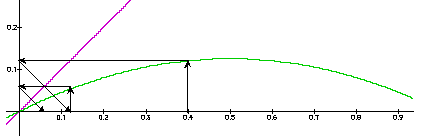


Attracteur : (0 ; 0)

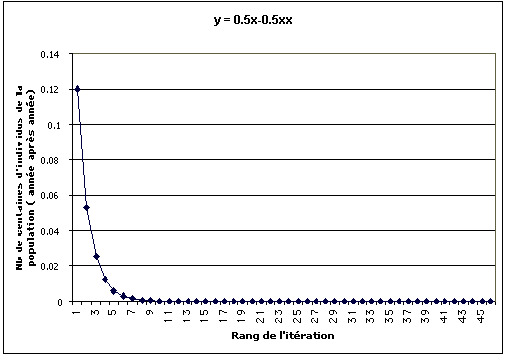
Convergence vers 0; extinction de la population

a = 2

attracteur (0.5, 0.5)

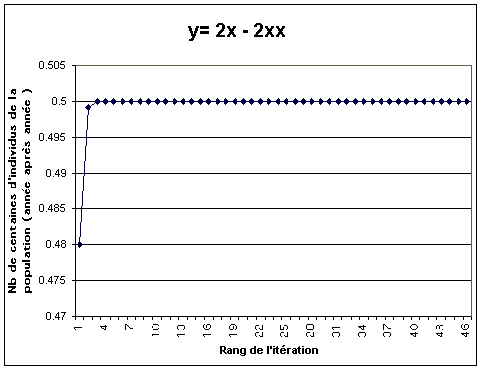
Convergence vers une solution : 0.5; Population en équilibre qui se stabilise vers une constante

a = 3

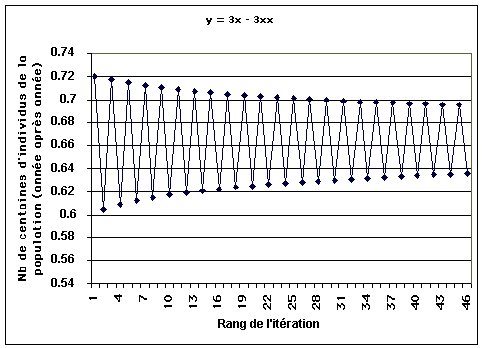
Convergence lente vers une solution : 0.666... ; Progression en douceur de la population vers un équilibre stable

a = 3.2

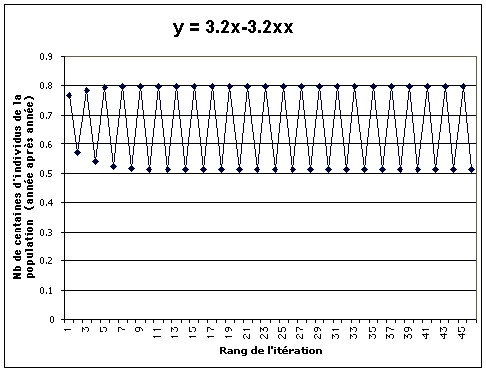
Convergence vers deux solutions : 0.799... 0.513... ; Alternance de deux quantités de populations en équilibre stable et constant

a = 3.5

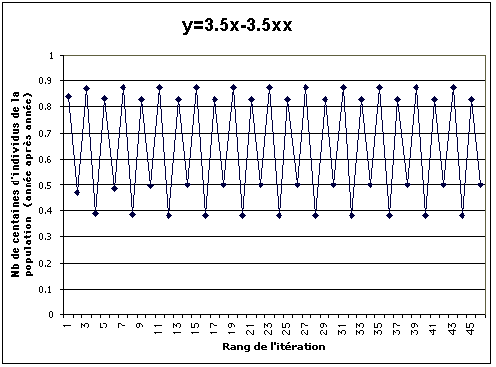
Convergence vers quatre solutions : 0.875... 0.826... 0.500...0.382... ; Cycle de quatre quantités de populations en équilibre stable et constant

a = 3.6

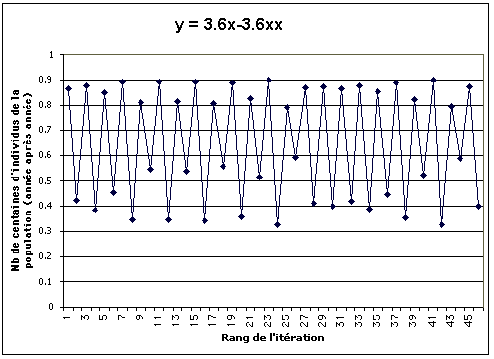
Convergence chaotique comprise entre une limite supérieure (liée aux coordonnées du sommet de la courbe) et une limite inférieure : infinité de solutions ?

Variation quantitative imprévisible de la population, bornée par un maximum et un minimum

a = 4

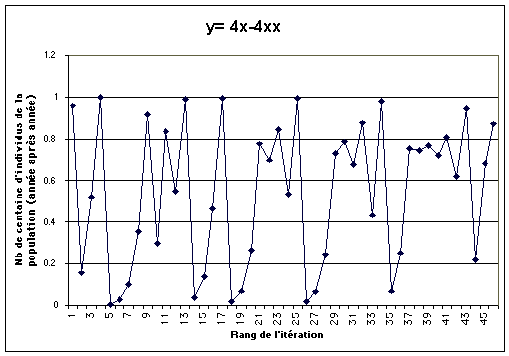
Convergence chaotique comprise entre la limite supérieur 1 et la limite inférieur 0 : infinité de solutions ?
Variation quantitative imprévisible de la population, bornée par le maximum 1 et le minimum 0

Résumé

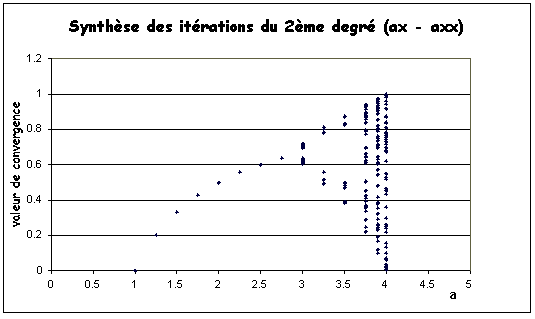
Commentaire

On a représenté ici qu'une petite partie des diagrammes réalisés chaque fois: « carte du premier retour » et relation de la valeur de x en fonction de n.

Les valeurs de a considérées sont: 0.5 et 1 (convergence vers 0); 2 (convergence croissante vers 0,5); 2,7 (convergence alternée vers 0.629...) ; 3 (convergence alternée lente vers 0.666...);

Pour a = 3.1, 3.2, 3.3, 3.4 on a une oscillation entre deux valeurs d'attraction. Un problème de désignation apparaît; peut-on parler de convergence ?

Pour a = 3.5 la période a doublé.

Avec a = 3.6, 3.7, 3.8, 3.9 et 4 apparations de comportement bizzare.

Les outils à disposition ne permettent pas de voir des résurgences de cas périodiques.

Compléments théoriques

Chaos

Selon L. Nottale, on peut définir le chaos dynamique comme le comportement aléatoire se produisant dans certains systèmes déterministes, donc rien à voir avec le sens usuel du mot chaos, confusion, désordre, absence de loi. Le chaos est une propriété de certains systèmes déterministes, lesquels sont bien décrits par des lois.

C'est H. Poincaré qui découvrit qu'« un système décrit par des lois déterministes peut avoir un comportement relevant du hasard ». Le chaos se caractérise par une haute sensibilité aux conditions initiales. C'est « l'effet papillon » découvert en 1963 par le météorologue E. Lorenz. L'écart final peut atteindre rapidement des proportions énormes. Un système chaotique est donc limité par un horizon temporel de prédictibilité. Une prédiction à long terme est illusoire et une prédiction à court terme s'exprimera à l'aide de probabilités. C'est ce qui fait que l'on peut parler d'ordre dans le chaos. Le climat est un système chaotique, et l'on connaît l'imprédictibilité des prévisions météorologiques à long terme. Par contre on peut davantage se fier aux prévisions à court terme, mais la sensibilité aux conditions initiales du climat ne permet pas d'assurer une prévision météorologique certaine, on recourt alors à une prédiction en termes de probabilité.

Un système chaotique évolue toujours vers son attracteur (parfois qualifié d'étrange). De tels attracteurs sont souvent fractals, comme l'attracteur étrange fractal de E. Lorenz (Voir le graphique). Le climat est un système chaotique. Sa convergence correspond à un processus de convection atmosphérique qui produit au hasard, des successions de différents types de climat relativement similaires, évitant les changements climatiques extrêmes.

Historique de la science du chaos

La fonction y = a x ( 1- x) (pour les valeurs de a comprises entre 0 et 4) est nommée fonction logistique par les biologistes. Il s'agit d'un modèle de croissance de population qui est chaotique pour certaines valeurs de a.

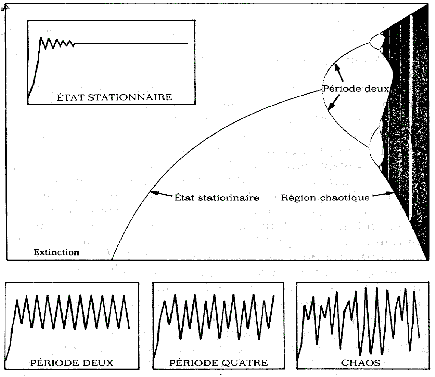
En fait , c'est environ à partir de la valeur a = 3,57 que se produit une bifurcation entre deux dynamiques très différentes (Lehning, 2000).

C'est Robert May, biologiste américain, qui découvre les bifurcations (voir le graphique) ainsi que la sensibilité aux conditions initiales de la fonction logistique. Une toute petite variation des paramètres a ou x produisent des explosions démographiques de populations ou des extinctions massives, d'où la difficulté de faire des pronostics à long terme concernant l'évolution démographique d'une population.

La formule de la fonction logistique correspond à une « virtualité  écologique » plutôt qu'à une « réalité biologique». L'informatique permet de jouer avec les paramètres de la formule afin de découvrir la nature de l'évolution de la population en interaction avec son environnement.

C'est une simulation de la réalité d'une population (la biocénose) se développant dans un habitat (le biotope) dont les ressources alimentaires (l'énergie ) sont naturellement limitées.

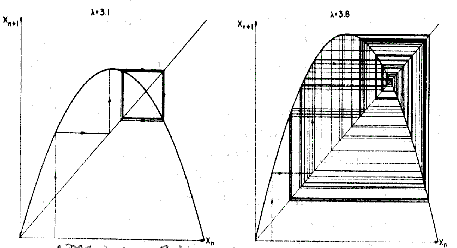
C'est Mitchell Feigenbaum, mathématicien américain, qui découvre et explore le chaos au moyen de la fonction logistique. Il décrit le chaos qui succède aux bifurcations, dans lequel il découvre quelques éléments d'ordre comme les attracteurs étranges. Il démontre aussi que tout système chaotique converge vers son attracteur(voir graphiques).

Feigenbaum a élaboré la théorie du chaos qui présentait pour la première fois la transition d'un comportement périodique régulier vers le chaos. Elle nous enseigne aujourd'hui comment des systèmes simples, telle que la fonction logistique, peuvent avoir des comportements imprévisibles.

Références

Gleick, J. (1987).  La théorie du chaos. Paris : Flammarion.
Nottale, L. (1998). La relativité dans tous ses états. Paris : Hachette.
Bergé, P. &t al. (1997). Des rythmes au chaos. Paris : Opus.
Mandelbrot, B. (1997). Fractales, hasard et finance. Paris : Flammarion.
Poincaré, H. (1968). La science et l'hypothèse. Paris : Flammarion.
Bak, B. (1996). Quand la nature s'organise. Paris : Flammarion.
Lehning, H. (2000). Nouvelles tendances : chaos. Tangente, Hors série n°10.