Société des enseignants
neuchâtelois de sciences (SENS)
BULLETIN No 23 / Astronomie
Le géocentrisme de Ptolémée
et l'héliocentrisme de Copernic
Gaston Fischer, Rue de Rugin 1A, CH-2034 Peseux, gfischer@vtx.ch
Dans un récent article d'ORION Andreas Verdun [1] fait l'historique des événements qui ont culminé avec la publication de De revolutionibus orbium coelestium et il présente une biographie de son auteur Copernic. On trouvera une biographie beaucoup plus détaillée mais bien moins flatteuse dans le livre Les somnambules d'Arthur Koestler [2].
Il est bien connu que plusieurs savants grecs avaient déjà proposé un système héliocentrique, en particulier Aristarque de Samos (~310 - ~230 av. J.-C.) et Seleucus (IIième s. av. J.-C.). Aristarque avait eu un grand renom d'astronome, mais il fut suivi par Hipparque de Nicée (~190 - ~120 av. J.-C.), dont la réputation fut plus grande encore. On doit par exemple à Hipparque le premier traité systématique de trigonométrie et le premier catalogue de 850 étoiles. Ses observations étaient connues pour leur précision et en les combinant avec les archives d'observations faites par des prédécesseurs à Babylone et Alexandrie, il découvrit la précession des équinoxes et put déterminer la longueur du mois lunaire à la seconde près. A cause de l'absence d'une parallaxe observable il rejeta l'idée d'un monde héliocentrique.
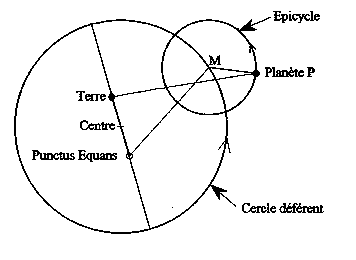
On admet généralement que c'est à cause du renom d'Hipparque que la conception géocentrique du monde s'imposa avec autorité et qu'elle perdura pendant plus de 1600 ans [c.f. p.ex. 3]. Mais une deuxième raison, plus importante encore, pourrait bien avoir engendré cette remarquable pérennité : c'est la qualité du système proposé par Ptolémée (~100 - ~ 165 ap. J.-C.). Le système de Ptolémée est bien connu, spécialement celui concernant les planètes extérieures, reproduit à la Fig. 1. Pour les planètes intérieures Ptolémée eut besoin d'un système nettement plus compliqué [c.f. p.ex. 4] qui ne sera pas considéré ici.
|
Figure 1. Construction de Ptolémée, entièrement basée sur des cercles, pour les orbites des planètes supérieures, Mars, Jupiter et Saturne. La planète tourne à vitesse angulaire constante dans le sens indiqué sur le cercle de l'épicycle, dont le centre M est en orbite sur le cercle déférent. La vitesse de M n'est pas uniforme sur le cercle déférent; par contre, la vitesse angulaire de ce point est uniforme par rapport au Punctus Equans, décentré d'un segment appelé équant. L'équant est symétrique au décentrage de la Terre par rapport au centre. La rotation de la planète sur l'épicycle est nécessaire pour compenser la rotation de la Terre autour du Soleil et se fait donc exactement sur un an. La parallèle au segment MP par le centre du cercle déférent est dirigé vers le Soleil. Les points décentrés, "Terre" et "Punctus Equans", correspondent manifestement aux foyers des ellipses képleriennes. Le passage à un système héliocentrique verrait la planète au point M et le Soleil à la place de la Terre. |
Dans le diagramme de la Fig. 1 le rôle de l'épicycle est de reproduire la rétrogradation observée pour les planètes, rétrogradation causée par la rotation de la Terre autour du Soleil : la planète fait un tour d'épicycle à vitesse constante chaque fois que la Terre parcourt une fois sa propre orbite. Si, à ce stade, Ptolémée était passé à un système héliocentrique, il aurait placé le Soleil à la position marquée "Terre" dans la figure et la planète au point M ; il n'aurait plus, alors, eu besoin d'un épicycle. D'autre part, en décentrant la position du Soleil, Ptolémée s'était rapproché d'un système képlerien et le seul pas qu'il aurait encore eu à franchir était le passage du cercle à l'ellipse.
Il est bien connu que Ptolémée n'a pas fait ce pas, mais l'a remplacé par un autre dont nous allons étudier les mérites. Comme indiqué à la Fig.1, le point M se déplace sur le cercle déférent; mais sa vitesse n'y est pas uniforme. Au contraire, cette vitesse semble être uniforme lorsqu'elle est vue depuis le Punctus Equans , un point introduit par Ptolémée en position symétrique du point "Terre" par rapport au centre du cercle déférent. Exprimé de façon plus simple, on dit que la vitesse angulaire du point M est uniforme par rapport au Punctus Equans . Ici on pourrait faire la remarque qu'en se limitant à des distances symétriques par rapport au centre, Ptolémée se privait d'un degré de liberté additionnel. Mais nous allons voir que son choix est en fait le meilleur possible.
Dans la théorie képlerienne des orbites planétaires,
la deuxième loi est celle des aires. Selon cette loi, les aires
des secteurs orbitaux balayés par le rayon entre Soleil et planète
sont proportionnelles aux intervalles de temps correspondants. Cela
signifie que, vue depuis le Soleil la planète se déplace
plus vite si sa distance au Soleil est plus courte. Au périgée
de son orbite la planète a donc sa plus grande vitesse et à
l'apogée la vitesse la plus petite. Par la loi des aires on trouve
facilement les vitesses orbitales 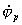 et
et 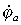 au périgée
et à l'apogée :
au périgée
et à l'apogée :
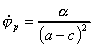 et et
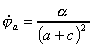 |
(1)
|
a est le demi grand-axe et c la distance focale, cette
distance étant généralement exprimée au
moyen de l'excentricité ![]() , soit c =
, soit c = ![]() . a
, selon la Fig.2.
. a
, selon la Fig.2.
La constante a des équations (1) se déduit aisément
de la troisième loi de Képler (T2/a3
= 4p2/GM) qui met en relation le carré de la
période orbitale T et le cube du demi grand-axe a
:
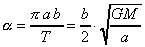 |
(2)
|
où b est le demi petit-axe, G la constante de la gravitation et M la masse du Soleil.
En général on n'attribue pas de signification particulière
au second foyer; mais si on se place à cet endroit pour suivre
le mouvement orbital de la planète, il est évident que
la vitesse angulaire que l'on observe depuis ce point sera plus uniforme
que celle qu'on voit depuis le Soleil. Cette observation est facile
à confirmer; il suffit de multiplier les vitesses orbitales données
en (1) par le rapport des rayons, (a - c)/(a + c) au périgée
et (a + c)/(a - c) à l'apogée. On trouve
alors le résultat un peu surprenant que ces deux vitesses orbitales,
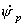 et
et 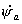 , sont identiques :
, sont identiques :
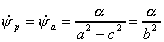 |
(3)
|
Par un calcul similaire on montre qu'aux extrémités des petits axes les vitesses angulaires vues depuis les deux foyers sont toujours égales à
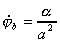 |
(4)
|
La symétrie (ou l'antisymétrie !) de ces résultats
est remarquable et on note que les vitesses orbitales observées
depuis le second foyer sont un peu plus petites aux extrémités
des petits axes qu'à celles des grands axes. Mais dans le cas
le plus défavorable des 5 planètes connues du temps de
Ptolémée, celui de Mercure dont l'excentricité
![]() = 0.206 , on trouve
= 0.206 , on trouve
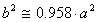 |
(5)
|
Même pour Pluton, avec ![]() = 0.249 , on a
= 0.249 , on a
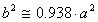 |
(6)
|
alors que pour Mars, la planète extérieure de plus grande
excentricité connue de Ptolémée avec ![]() = 0.093 , il vient
= 0.093 , il vient
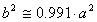 |
(7)
|
Ces résultats apportent la confirmation que la propriété attribuée par Ptolémée au Punctus Equans, selon laquelle depuis ce point le rayon orbital du point M se déplace de façon uniforme sur le cercle déférent, est presque parfaitement réalisée.
On pourrait maintenant reprocher à Ptolémée d'avoir
choisi pour ses épicycles et ses déférents des
cercles et non pas des ellipses. Cela est certainement vrai; mais les
déformations requises pour l'épicycle ne serviraient qu'à
compenser la déformation elliptique de l'orbite de la Terre,
dont l'excentricité n'est que de ![]() = 0.017 . Quant au cercles déférents, nous venons de voir
que parmi les planètes connues de Ptolémée, à
l'exception de Mercure elles avaient toutes de très petites excentricités.
D'autre part, il est bien connu que l'excentricité ne décrit
pas bien l'écart qu'il y a entre un cercle et une ellipse. Comme
le montre la Fig. 2, l'excentricité
= 0.017 . Quant au cercles déférents, nous venons de voir
que parmi les planètes connues de Ptolémée, à
l'exception de Mercure elles avaient toutes de très petites excentricités.
D'autre part, il est bien connu que l'excentricité ne décrit
pas bien l'écart qu'il y a entre un cercle et une ellipse. Comme
le montre la Fig. 2, l'excentricité ![]() est une mesure de la distance qu'il y a entre le centre de l'ellipse
et les foyers. Exprimée au moyen des demi axes a et b
de l'ellipse,
est une mesure de la distance qu'il y a entre le centre de l'ellipse
et les foyers. Exprimée au moyen des demi axes a et b
de l'ellipse, ![]() s'écrit
:
s'écrit
:
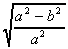 |
(8)
|
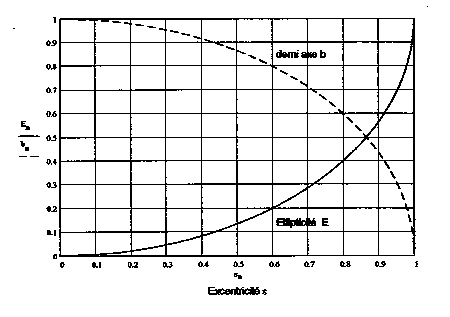
Comme suggéré à la Fig. 2 et confirmé
par la Fig. 3, la valeur de l'excentricité ![]() donne une image exagérée de la déformation elliptique.
En effet, si on considère l'ellipse comme un cercle aplati, un
bien meilleur paramètre pour décrire cette déformation
est le raccourcissement du petit-axe par rapport au grand-axe, ce que
nous décrirons par un paramètre que nous appelons ellipticité
E :
donne une image exagérée de la déformation elliptique.
En effet, si on considère l'ellipse comme un cercle aplati, un
bien meilleur paramètre pour décrire cette déformation
est le raccourcissement du petit-axe par rapport au grand-axe, ce que
nous décrirons par un paramètre que nous appelons ellipticité
E :
|
E =
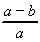 |
(9)
|
|
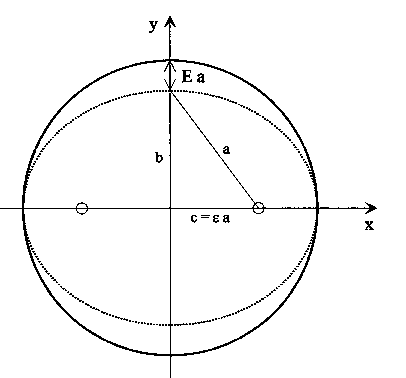
Figure 2. Cercle
et ellipse inscrite de demi grand-axe a . L'excentricité
|
Dans l'exemple de la Fig. 2 on voit qu'à une excentricité
![]() = 0.6 ne correspond qu'une ellipticité E = 0.2 . La Fig. 3 ,
qui est une représentation de l'ellipticité E en fonction
de l'excentricité
= 0.6 ne correspond qu'une ellipticité E = 0.2 . La Fig. 3 ,
qui est une représentation de l'ellipticité E en fonction
de l'excentricité ![]() ,
illustre notre argument : pour des excentricités
,
illustre notre argument : pour des excentricités ![]() inférieures à 0.1 , l'ellipticité est toujours
inférieure à E
inférieures à 0.1 , l'ellipticité est toujours
inférieure à E ![]() 0.005 et dans ces conditions il sera difficile de voir qu'une ellipse
d'excentricité
0.005 et dans ces conditions il sera difficile de voir qu'une ellipse
d'excentricité ![]()
![]() 0.1 est vraiment une
ellipse et non pas un cercle. Pour la Terre, avec
0.1 est vraiment une
ellipse et non pas un cercle. Pour la Terre, avec ![]() = 0.017 on obtient E = 0.0001445 , et la déformation requise
pour l'épicycle serait donc vraiment négligeable. On sait
cependant que l'excentricité des planètes évolue
avec le temps; mais les périodes typiques de ces variations sont
de l'ordre de dizaines à centaines de milliers d'années.
= 0.017 on obtient E = 0.0001445 , et la déformation requise
pour l'épicycle serait donc vraiment négligeable. On sait
cependant que l'excentricité des planètes évolue
avec le temps; mais les périodes typiques de ces variations sont
de l'ordre de dizaines à centaines de milliers d'années.
|
Figure 3. Représentation
de l'ellipticité E et de la longueur réduite du
demi petit-axe b/a en fonction de l'excentricité |
Les arguments présentés démontrent que le système imaginé par Ptolémée pour décrire les orbites des planètes est finalement très proche de la représentation képlerienne. Comme nous l'avons dit au début, ce système est si bien adapté à la réalité qu'il a sûrement contribué à sa pérennité pendant 1300 ans. De fait, il est bien connu que le système tel que l'a proposé Copernic était moins élégant que celui de Ptolémée, ceci pour différentes raisons :
1) Le passage du système géocentrique à l'héliocentrique a certes permis à Copernic de se débarrasser de l'épicycle. Comme on le sait, les philosophes grecs avaient choisi d'expliquer le ciel en se limitant à l'utilisation de cercles et de sphères; à leurs yeux ces figures géométriques étaient les plus parfaites, celles de plus haute symétrie, sans début et sans fin. Il était inadmissible de penser que les divinités responsables de la genèse du monde aient pu le construire avec des élément de perfection inférieure. Même s'il ne partageait peut-être pas les mêmes raisons de se limiter à l'emploi de cercles pour décrire le mouvement des planètes, Copernic n'eût pas l'imagination de se débarrasser de cette tradition arbitraire. Mais l'héliocentrisme le plus primitif ignore le décentrage des orbites; pour remédier à l'absence de décentrage Copernic fut obligé d'introduire des petits cercles correcteurs et cela compliquait son système.
2) Copernic fit une deuxième erreur de jugement. Ayant admis que le Soleil était l'astre majeur gouvernant la marche des planètes, il n'en fit pourtant pas le centre de son système. Une fois encore il témoigna d'un grand manque d'imagination, choisissant pour point d'encrage le centre de l'orbite de la Terre. Il se vit alors une nouvelle fois obligé de compenser cette inconsistance par l'introduction de petits cercles correcteurs.
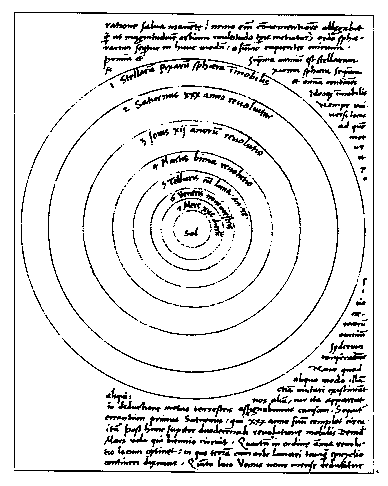
En définitive, le système proposé par Copernic, s'il n'avait plus besoin d'un grand épicycle pour compenser la rotation de la Terre autour du Soleil, nécessitait davantage de petits cercles correcteurs que celui de Ptolémée [4,2] ! On en trouve une confirmation indirecte dans le manuscrit de Copernic, dont une page, tirée de l'article de Verdun [1], est reproduite à la Fig. 4.
|
Figure 4. Reproduction d'une page du manuscrit de Copernic, dans lequel il décrit son système héliocentrique. Le Soleil est au centre autour duquel gravitent les planètes. Mais les cercles n'en sont pas les orbites, ils délimitent seulement les zones attribuées à ces orbites, dont la forme exacte est beaucoup plus compliquée. |
A bien des égards, l'ensemble des lois de Képler constituent
une révolution plus importante que l'héliocentrisme de
Copernic. Avec Képler on a non seulement la vraie géométrie
des orbites, mais encore la cinématique correcte des planètes.
Ptolémée a plusieurs fois été accusé de fraude. Il aurait manipulé des données mesurées afin d'améliorer la correspondance avec sa théorie. Cette question vient d'être revue par Hetherington [5] qui ne pense pas que ce reproche soit justifié. Selon Hetherington on ne peut pas juger Ptolémée selon les critères acceptés aujourd'hui pour ce qu'on considère comme l'éthique scientifique. Du temps de Ptolémée on n'avait pas encore développé les notions de répartition statistique des données. Au lieu de traiter l'ensemble des mesures par des techniques statistiques, il est probable que Ptolémée choisit celles qui illustraient le mieux sa théorie, cela d'autant plus que son ouvrage avait un but éminemment didactique.
Références
[1] Verdun Andreas : Eine astronomische Revolution vor 500 Jahren ? ORION, No. 297, avril 2000, pp. 4-9.
[2] Koestler Arthur : Les somnambules, traduction de The Sleepwalkers. Penguin, 1959, first published by Hutchinson, London, 1954.
[3] Lovell Bernard : Emerging Cosmology. Praeger, New York, 1985. ISBN 0-03-001009-8.
[4] North John : Astronomy and Cosmology. Fontana, London, 1994. ISBN 000686177 6.
[5] Hetherington Noriss S. : Ptolemy : on trial for fraud, Astronomy & Geophysics, 38/2, 1997, pp. 2427.