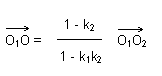1) Les questions du secondaire I

Quelle place convient-il de réserver ou non aux vecteurs dans les dernières années de la scolarité obligatoire ? Qu'il s'agisse d'aménager les programmes ou de les appliquer en classe, des maîtres s'interrogent : Est-il si indispensable d'introduire les opérations sur les vecteurs ? Ne laisse-t-on pas ensuite ces notions mariner dans l'esprit des élèves jusqu'à ce que le secondaire II en tire profit ? Toujours à l'affût d'un éventuel gain de temps, on se demande si l'étude des translations ne suffirait pas dans le cadre des transformations du plan.

Il est vrai que lorsqu'on aborde les vecteurs, c'est souvent comme une sorte d'appendice aux translations et peut-être sans grande motivation. A cela rien d'étonnant: translations et vecteurs sont deux aspects d'une même réalité. Dit en langage mathématique, la composition des translations est isomorphe à l'addition des vecteurs. Ce sont deux exemples d'une même structure de groupe commutatif.

On ne peut tenter de répondre raisonnablement à ces questions sans évoquer le développement historique de la géométrie élémentaire et ses conséquences pour l'enseignement.

2) Le poids de la géométrie euclidienne

On ne dit rien de très nouveau en rappelant que la géométrie tire son origine des "Eléments" d'Euclide qui datent d'environ trois cents ans avant Jésus-Christ. En revanche, il peut paraître surprenant que cette influence ait perduré jusqu'au XX ème siècle, sinon dans sa forme, tout au moins dans son esprit. En voici un exemple : A la fin du XIXème siècle, Jacques HADAMARD (1865 ­ 1963) publie ses "Leçons de géométrie élémentaire". Cet ouvrage de plus de mille pages réparties en deux volumes sera la référence de l'enseignement français pendant un demi­siècle au moins puisque la treizième édition paraît en 1947 !

Les intentions d'Hadamard sont claires; il les exprime dans l'"Avertissement à la deuxième édition" :

"Depuis l'apparition de cet ouvrage, l'enseignement des mathématiques et, particulièrement, de la géométrie, a subi non seulement dans ses détails, mais dans tout son esprit, des modifications profondes depuis longtemps attendues et universellement réclamées. On tend à le faire reposer, pour les commençants, sur la pratique et l'intuition, et non plus sur la méthode euclidienne dont ils sont incapables de comprendre l'utilité.

Par contre, il est bien entendu qu'on revient à cette méthode lorsqu'il s'agit de revoir ces premiers débuts et de les compléter. "C'est à ce stade de l'enseignement que correspond notre livre et nous n'avions pas, par conséquent, à en changer le caractère." (c'est nous qui soulignons)

On ne trouve aucune trace dans ce traité de la notion de vecteur, aucun recours à la géométrie analytique et aux coordonnées. Il s'agit donc bien de "géométrie pure". Il vaut la peine de citer l'introduction de la translation, placée dans le chapitre des parallélogrammes et avant l'étude des droites concourantes dans le triangle (op.cit. p. 50­51) :

"Si, par tous les points d'une figure, on mène des droites égales, parallèles et de même sens, les extrémités de ces droites forment une figure égale à la première.( ... ) L'opération par laquelle on passe de la première figure à la seconde a reçu le nom de translation. On voit qu'une translation est déterminée quand on se donne en grandeur, direction et sens le segment tel que AA', qui va d'un point à son homologue."

La position d'Hadamard pourrait servir la cause de ceux qui prétendent que les vecteurs n'apportent rien de plus que les translations. Notons qu'Hadamard en reste là et ne s'intéresse pas pour autant à la composition des translations.

3) D'où viennent les vecteurs ?

Les vecteurs ne jouissent pas d'une lointaine origine comme la géométrie euclidienne. Bien au contraire. Il semble que c'est à WESSEL (1745­1818) que l'on doit un mémoire de 1799 où l'on trouve pour la première fois une addition de segments, analogue à ce que nous appelons aujourd'hui l'addition des vecteurs. Cette addition, conçue par analogie avec la composition des forces en physique, était destinée à légitimer l'addition des nombres complexes.

Mais ce n'est que plus tard qu'on a mis en évidence la structure de groupe de cette addition vectorielle. Il faut souligner à ce propos que jusque vers 1860, on ne s'intéressait qu'aux groupes de permutations d'un ensemble fini d'objets. C'est avec les travaux de Félix KLEIN (1849­1925) vers 1870 que naissent les groupes de transformations. Dès lors, c'est dans les traités classiques d'analyse qu'il faut aller chercher la théorie des vecteurs.

Compte tenu du décalage entre l'apparition d'une notion nouvelle en mathématiques et son enseignement dans les écoles, il n'y a pas lieu de s'étonner de l'absence des vecteurs dans les programmes scolaires jusqu'à la moitié du XX ème siècle. De même, les idées de Klein, exprimées dans le "Programme d'Erlangen" (1872) ont mis près d'un siècle pour atteindre l'enseignement élémentaire avec les transformations du plan: symétries, translations, rotations, homothéties et similitudes.

4) Triangle ou parallélogramme ?

On ne peut pas refaire l'histoire. Mais on peut imaginer ce qui serait advenu si les Grecs n'avaient pas privilégié le triangle en repoussant le plus tard possible ce qui touche au parallélisme. A ce propos, citons deux auteurs. D'abord Gustave CHOQUET dans son introduction à "L'enseignement de la géométrie" (1964) :

"On sait qu'Hilbert a élagué et complété l'axiomatique d'Euclide, pour en faire un système logiquement satisfaisant (...). L'axiomatique d'Hilbert-Euclide est basée sur les notions de longueur, d'angle, de triangle. Elle cache à merveille la structure vectorielle de l'espace, au point que de nombreux siècles ont ignoré la notion de vecteur. Le fait qu'un triangle soit la moitié d'un parallélogramme n'a pas empêché qu'on mette l'accent pendant plus de vingt siècles sur l'étude détaillée des hauteurs, médianes, médiatrices et bissectrices des triangles, sur les cas d'égalité des triangles et sur les relations métriques dans le triangle. On voyait le triangle, mais non le parallélogramme qui aurait pu conduire aux vecteurs."

On retrouve les mêmes considérations dans un langage plus poétique sous la plume de Michel SERRES dans "Les origines de la géométrie" (1993) :

"Supposé qu'Euclide et ses prédécesseurs aient considéré le triangle comme une moitié d'un carré ou mieux d'un parallélogramme, ils auraient été immédiatement conduits à la structure de l'espace des vecteurs.

Nous voici donc de nouveau, à l'origine, où nous reprenons un autre bon bout de l'histoire : le point, le segment, l'angle, puis le triangle ouvert, trois segments à sommet commun, partie de parallélogramme, et non le triangle fermé que nous nommons triangle, improprement; d'où l'on tire l'addition vectorielle, par composantes et résultante, ce qui, en retour, fait rejaillir, sur le segment, la notion à son tour principielle de vecteur, et, sur le point, celle du vecteur nul et ainsi de suite: la structure d'espace vectoriel se dévoile peu à peu, dans une simplicité première." (p. 20)

5) Proposition

En ce qui concerne les fonctions, le pas est déjà fait et avec profit. Il pourrait en être de même pour les vecteurs qui deviendraient un fil conducteur à travers tout l'enseignement secondaire (I et II). Bien sûr, cela demanderait un changement radical par rapport à la situation que nous connaissons. Il conviendrait de faire des vecteurs une notion de base, indépendante de la géométrie euclidienne. Expliquons-nous.

Un vecteur ne se réduit pas à la seule représentation initiale qu'on en donne sous forme de flèche ayant une direction, une longueur et un sens. Un vecteur, c'est un élément d'un espace vectoriel. Cette formulation n'a rien d'une lapalissade : Un espace vectoriel est un ensemble dont on peut additionner les éléments (avec les propriétés d'un groupe commutatif) et dont on peut multiplier les éléments par des nombres (avec des propriétés naturelles). Soit dit en passant, ces propriétés sont si naturelles que les élèves les utilisent avec habileté et fort peu d'erreurs.

Un exemple vaut mieux qu'un long développement :

Les carrés magiques d'ordre 3 forment un espace vectoriel :

(Rappelons qu'un carré est magique si la somme des termes est la même en lignes, en colonnes et dans les diagonales.)

L'addition de deux carrés magiques donne encore un carré magique :

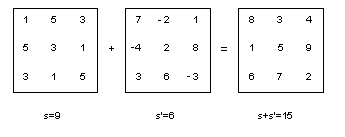
La multiplication d'un carré magique par un nombre donne encore un carré magique :

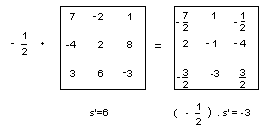
Serait-il abusif de voir une situation-problème dans l'énoncé suivant à proposer à des lycéens ?

N'importe quel carré magique C d'ordre 3 peut s'écrire comme combinaison linéaire de 3 carrés magiques bien choisis C1, C2, C3 :

Supposons :

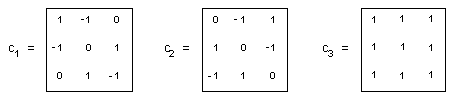
Alors :

Même si le maître de mathématiques introduit les vecteurs dans le cas particulier du plan, il doit se souvenir des nombreux exemples d'espaces vectoriels que sont les fonctions continues, les fonctions dérivables, les solutions d'équations linéaires, etc.

En faisant des vecteurs une notion fondamentale, il y aurait à éviter certains écueils qui pourraient faire échouer le projet. Nous en citons trois :

a) Vouloir "démontrer" les propriétés des vecteurs via la géométrie élémentaire. Le premier manuel paru en Suisse romande traitant des vecteurs est sans doute la "Trigonométrie" de PAULI et POST (1946). Destiné aux gymnasiens, il fait reposer les propriétés des vecteurs sur les connaissances de géométrie élémentaire acquises par les élèves dans la scolarité obligatoire. Ainsi, pour prouver que "deux vecteurs égaux ont des projections égales suivant un même axe", on fait intervenir des parallélogrammes et des trapèzes égaux. Cette méthodologie, légitime à l'époque pour le secondaire II, n'aurait pas sa place au secondaire I dans la perspective que nous envisageons.

b) Vouloir dès le début associer de trop près vecteurs et points du plan. On risque de masquer la vraie nature des vecteurs. Un vecteur n'est pas simplement assimilable à un couple de points, voire à un point unique après choix d'une origine. Le calcul vectoriel ne saurait se ramener uniquement à des opérations sur des bipoints telles qu'on les trouve dans les fascicules no 17 et no 23 de la CRM (Commission romande de mathématique). Nous reviendrons sur cette question à propos de la relation de Chasles.

c) Vouloir gagner du temps en laissant de côté des exercices pour se contenter d'écrire proprement des relations découlant des définitions. On doit proposer des situations qui aient du sens et montrent l'utilité et l'avantage du calcul vectoriel. Il serait précieux d'étudier comment articuler ce projet avec les tendances actuelles de la didactique, en particulier avec les problèmes ouverts et les situations-problèmes.

6) Suggestions

On ne peut suggérer dans le cadre de ce texte que les pistes principales pour un cheminement souhaitable dans l'introduction des vecteurs. L'articulation avec le reste du programme serait du ressort des maîtres qui voudraient bien en tenter l'expérience.

Première étape : L'addition vectorielle présentée comme la mise bout à bout de segments orientés ou "flèches". Des flèches parallèles, de même longueur et de même sens représentent le même vecteur. La figure ci-dessous illustre l'addition de deux vecteurs et la propriété de commutativité.

Deuxième étape : Présentation intuitive de la multiplication d'un vecteur par un nombre et ses propriétés naturelles.

On pourrait, par exemple, aborder la propriété de distributivité

par le biais d'un exercice :
On envisage deux vecteurs de directions différentes.

Construire :

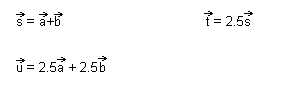
Est­il exact que ?

Insistons-y. Il n'y a pas à justifier une telle propriété par un recours quelconque au théorème de Thalès ou à des similitudes. Il s'agit d'une propriété admise au départ; admise en raison d'une certaine évidence et de son efficacité. Pour le mathématicien, c'est un axiome.

Troisième étape : Deux vecteurs quelconques du plan, de directions différentes, suffisent pour exprimer tous les autres vecteurs. C'est la décomposition d'un vecteur quelconque par rapport à deux vecteurs de base :

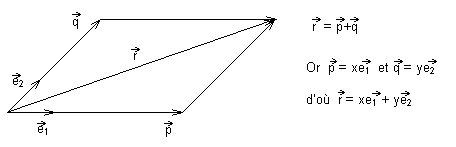
7) Exploitations possibles

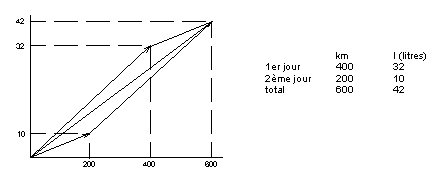
La structure d'espace vectoriel à deux dimensions étant ainsi présentée, il ne manque pas d'exercices pleins de sens. On a l'embarras du choix; il suffit d'adapter la difficulté au niveau de la classe. Exemple : consommation d'une auto sur deux jours

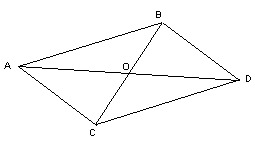
8) La relation de Chasles

Enfin, et seulement en fin, on introduira la relation de Chasles qui établit le lien entre vecteurs et points du plan. Pour en bien comprendre l'enjeu, il faut entrer dans quelques détails (à l'usage des maîtres). L'association entre vecteurs et points se présente en trois temps :

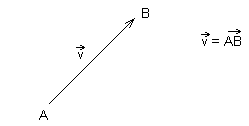
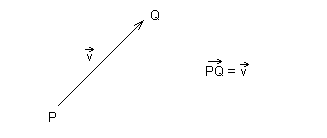
1) A tout couple de points du plan A et B, on associe un vecteur unique d'origine A et d'extrémité B. On note

2) Inversement, étant donné un point P et un vecteur , il existe un point unique Q tel que

3) Considérons un point P et deux vecteurs et . D'après 2, il existe Q tel que

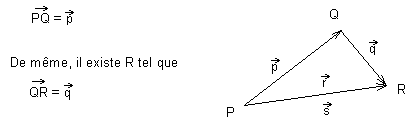
Soit

D'après 1) il existe un vecteur unique tel que

La relation de Chasles affirme que c'est-à-dire

Cette relation exprime le fait que l'association points­vecteurs est compatible avec l'addition vectorielle. Si l'on choisit un point 0 du plan comme origine et deux vecteurs comme base, on obtient un repère affine du plan (voir sous 6).

x et y sont les coordonnées de P dans ce repère.

Le vecteur d'origine A et d'extrémité B s'écrit:

La relation de Chasles ouvre le champ à toute la géométrie analytique.

En voici une utilisation classique:

"Les milieux des côtés d'un quadrilatère quelconque sont les sommets d'un parallélogramme". (Voir Math-Ecole 188, p. 16)

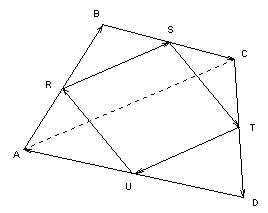
ABCD est un quadrilatère fermé. Cela implique :

Le parallélogramme RTSU est aussi un quadrilatère fermé:

De plus, deux côtés opposés sont parallèles et égaux:

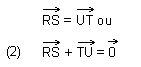
En tenant compte de (1'), on a aussi

Etablissons la démonstration:

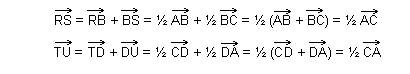
d'où:

9) Les dilatations (homothéties et translations)

Une fois établi le calcul vectoriel et la relation de Chasles pour le plan, on peut aborder des transformations du plan avec un outil efficace. Cette étude commencée intuitivement au secondaire I avec les homothéties trouverait son accomplissement au lycée. Ce thème serait ainsi repris, consolidé, approfondi.

Nous nous en tenons à deux exemples.

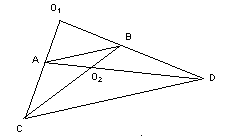
a) Un problème

On donne deux segments parallèles AB et CD. Quelles sont les homothéties qui permettent de passer d'un segment à l'autre ?

k est le nombre tel que

En général il y a quatre solutions:

Deux homothéties de centre 0₁ :

Deux homothéties de centre 0₂ :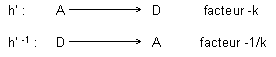


Au niveau supérieur, il est possible de préciser la position des centres 0₁ et 0₂ à l'aide des données.

Par exemple pour h, de :

on tire :

A ne pas oublier le cas particulier où AB et CD sont de même longueur. Il n'y a plus que trois solutions: deux translations (les voilà, enfin!) et une symétrie centrale (homothétie de facteur ­1).

b) Composition de deux homothéties

Si on compose deux homothéties h₁ de centre O₁ et h₂ de centre O₂, les facteurs d'homothéties étant k₁ et k₂, il n'est pas évident pour des débutants que le résultat fasse intervenir le produit k₁k₂. Il ne va pas de soi, non plus, que le centre de l'homothétie composée se trouve sur la droite O₁O₂ (pour autant que la composition ne soit pas une translation).

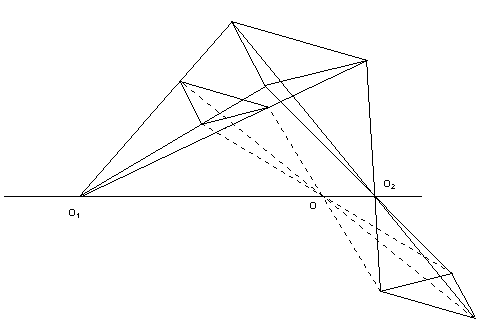
Là encore, on réservera au lycée le calcul de la position du centre O sur la droite O₁O₂ :