Société des enseignants
neuchâtelois de sciences(SENS)
BULLETIN No 22 / Note
Les nombres de Catalan
André Ammann, Yverdon
Les nombres de Catalan, exprimés par
![]()
![]()
sont probablement les nombres combinatoires apparaissant le plus fréquemment après les coefficients binomiaux. Quelques unes des multiples définitions de Cn sont :
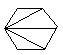
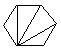
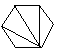
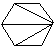
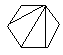
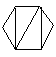
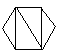
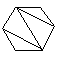
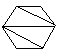
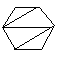
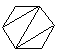
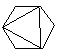
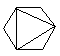
(i) Le nombre de façons de découper un polygone de n+2 côtés en n triangles, en dessinant n-1 diagonales ne présentant pas d'intersection entre elles.
| C1 =1 | |||||
| C2 =2 | |||||
| C3 =5 | 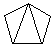 |
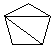 |
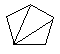 |
 |
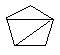 |
| C4=14 | 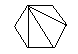 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
(ii) Le nombres de façons d'insérer des parenthèses dans un produit de n+1 lettres (de manière à ce qu'il y ait deux facteurs à l'intérieur de chaque paire de parenthèses).
n=1 (ab) ;
n=2 a(bc) , (ab)c ;
n=3 (ab)(cd) , a((bc)d) , ((ab)c)d , a(b(cd)) , (a(bc))d.
(iii) Le nombre d'arbres planaires binaires possédant n noeuds.
| C1 =1 | |||||
| C2 =2 | |||||
| C3 =5 |
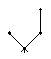
(iv) Le nombre d'arbres planaires avec racine possédant n noeuds.
| C1 =1 | |||||
| C2 =2 | |||||
| C3 =5 | 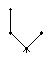 |
 |
(v) Lors d'une élection avec deux candidats A et B, chacun recevant n votes, Cn est le nombre de possibilités qu'ont les votes d'entrer de façon à ce que A ne soit jamais derrière B.