Société des enseignants
neuchâtelois de sciences (SENS)
BULLETIN No 22 / Didactique
Néo-darwinisme et théorie des jeux
Jean-Philippe Antonietti, Institut de Mathématiques Appliquées, Faculté des SSP, Université de Lausanne, BFSH 2, CH-1015 Lausanne. jean-philippe.antonietti@ip.unil.ch.
Proposez à vos élèves un nouveau jeu de pure réflexion
qui se joue à deux et à découvert. Incitez-les
à rencontrer un maximum d'adversaires. Dans ces conditions, il
y a fort à parier que leur façon de jouer va se modifier.
Si initialement toutes les actions permises par les règles du
jeu leur paraissent équivalentes, avec l'expérience certains
choix leur sembleront plus judicieux que d'autres. Ils découvriront
que certains coups leur assurent la victoire alors que d'autres les
condamnent irrémédiablement à la défaite.
Comment pourrait-on schématiquement décrire l'évolution
de leurs connaissances du jeu et rendre compte de l'amélioration
de leurs stratégies ? Nous allons dans cet article tenter
de répondre à cette question.
Toutes proportions gardées, cette interrogation est analogue
à celle qui fut à l'origine de toute l'oeuvre de Piaget
et l'on sait quelle solution il proposa. A l'instar de l'auteur de Biologie
et Connaissance nous recourrons à la notion fondamentale
d'adaptation qu'il faut interpréter comme " […] le
produit de réponses actives, autrement dit de régulations
compensatrices opérant par recombinaisons constructives et par
ajustement de réponses efficaces données aux problèmes
soulevés par le milieu." (Piaget, 1967, p. 68).
A cette fin nous représenterons les diverses stratégies
des élèves par des chromosomes qui, ensemble, constitueront
une population susceptible d'évoluer. Les transformations que
subira la population de génération en génération,
seront une imitation des mécanismes génétiques
naturels dont les principaux sont la reproduction, le croisement et
la mutation.
La reproduction est l'opérateur le plus important, c'est par
son entremise que s'effectue la sélection. Les individus les
plus aptes, ceux dont les performances sont les meilleures, ceux qui,
en l'occurrence, gagnent le plus souvent, auront plus de chance de se
reproduire; les moins bons disparaîtront. Mais cet opérateur,
bien que primordial, ne peut pas créer de nouveaux individus.
Afin de générer au sein de la population une certaine
variété il est nécessaire de recourir au croisement.
Un croisement s'effectue en deux temps. Des couples de chromosomes sont
formés aléatoirement puis s'échangent au hasard
des fragments d'information (voir fig1).
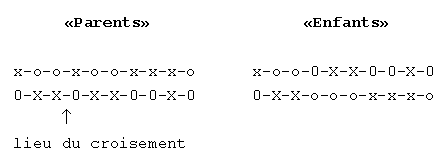
fig. 1. Le croisement
Suite au jeu de la reproduction et du croisement, il arrive
parfois que certaines informations potentiellement utiles disparaissent
du pool génétique de la population; ces dernières
peuvent être éventuellement réintroduites grâce
à une mutation. Ce troisième opérateur, qui ne
se déclenche que très rarement, modifie aléatoirement
l'un ou l'autre des gènes d'un chromosome.
Nous usons ainsi d'une métaphore biologique en comparant l'évolution
de la compréhension qu'ont les élèves d'un jeu
à l'évolution des espèces. Nous nous référons
donc directement au néo-darwinisme (1).
Cette théorie synthétique de l'évolution est une
intégration du darwinisme de Darwin à la théorie
génétique moderne, telle qu'elle résulte des lois
de Mendel. C'est ce qui constitue le champ d'investigation de la "génétique
des populations", créée à peu près
simultanément par Wright et Fisher, qui fournirent un certain
nombre de modèles mathématiques rendant compte de l'évolution
en utilisant d'une part les lois de Mendel, et d'autre par des coefficients
de sélection. Cette approche consiste à reconnaître
que les caractères sont déterminés par des gènes
et que ces gènes peuvent subir des mutations. Ainsi apparaissent
un certain nombre de différences entre individus d'une même
espèce. A travers le polymorphisme ainsi créé,
la sélection naturelle opère en éliminant ou au
contraire privilégiant tel individu porteur de tel gène.
Cela suppose donc que la mutation précède la sélection,
mais n'implique aucun lien entre l'agent mutagène et les conditions
de la sélection. L'intervention de la sélection naturelle
dans les processus évolutifs se fait donc, répétons-le
en deux temps: diversification génétique (par mutations,
recombinaisons ou autres événements aléatoires),
puis mise en ordre de la variabilité par la sélection
proprement dite. Dans le premier temps, le hasard joue le rôle
principal: les variations qui apparaissent ne sont pas systématiquement
adaptatives et leur apparition elle-même est indépendante
des conditions du milieu. Au cours de la deuxième étape
s'opère la sélection proprement dite, agent organisateur
extrinsèque. Dans une population de milliers ou de millions d'individus
tous différents, certains génotypes sont particulièrement
avantageux dans les conditions écologiques du moment: statistiquement,
ils ont plus de chance que les autres de survivre et d'engendrer une
descendance. C'est dans ce deuxième temps que l'évolution
trouve son orientation: les fréquences des gènes, ou des
combinaisons de gènes les plus favorables, à un instant
donné et en un lieu donné, augmentent, l'adaptation de
la population au milieu dans lequel elle vit se perfectionne; ainsi
apparaissent des spécialisations; ainsi se développent
des radiations adaptatives; ainsi se réalise ce qu'on a l'habitude
d'appeler le progrès évolutif.
L'idée de créer de tels systèmes artificiels fondés
sur les mécanismes de la sélection naturelle et de la
génétique est due à Holland. C'est dans son livre
originel intitulé Adaptation in natural and artificial systems,
publié en 1975, qu'il posa le cadre général de
l'étude de ce que l'on nomme actuellement les algorithmes génétiques
(2).
Afin d'être plus explicite, appliquons ce modèle à
l'étude du jeu des triplets (Gardner, 1986, p. 105). Ce jeu se
joue sur une bande formée de n cases avec des pions d'un
seul type. Les joueurs A et B déposent chacun à leur tour
un pion sur une case jusqu'à ce que l'un des joueurs gagne en
alignant trois pions adjacents. La figure 2 montre une partie gagnée
par B sur un terrain formé de 6 cases.
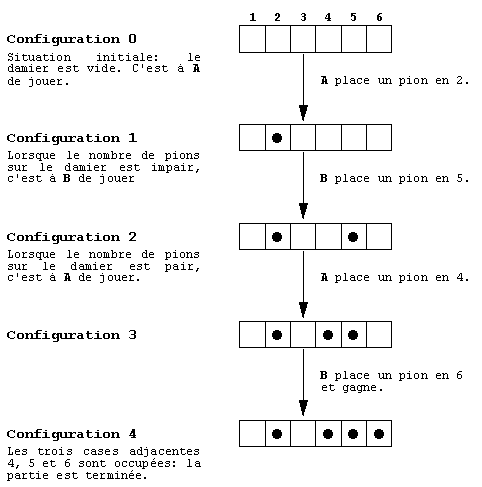
fig. 2. Exemple d'une partie gagnée par B sur un terrain
formé de 6 cases.
Comment définir les stratégies puis conséquemment les chromosomes ? Pour définir une stratégie, il suffit simplement de préciser pour chaque situation que peut rencontrer un joueur l'action qu'il exécuterait. Comment transformer cette information en un semblant de chromosome ? Rappelons qu'un chromosome est une très longue molécule d'acide déoxyribonucléique (ADN) qui renferme toute l'information génétique de la cellule et que cette information est codée linéairement à l'aide de quatre types de bases nucléotidiques: l'adénine (A), la cytosine (C), la guanine (G) et la thymine (T). Formellement, un chromosome n'est donc rien d'autre qu'une chaîne de caractères, un très long mot, composé à l'aide d'un alphabet restreint de quatre lettres. Pour donner à une stratégie une forme analogue, il faut commencer par définir un alphabet. Dans notre exemple, celui-ci sera constitué par les nombres 1 à n qui correspondent au coup permis. Puis il suffit de concaténer autant de caractères que de configurations possibles du jeu. Dans une cellule le code génétique s'exprime en deux étapes: dans un premier temps, la séquence des bases nucléotidiques d'un brin de la double hélice d'ADN est transcrite en un brin complémentaire d'acide ribonucléique (ARN) messager; dans un second temps, l'ARN messager est traduit en protéine. Pour extraire l'information d'un "chromosome-stratégie", il faut recourir à une table de conversion qui assigne à chaque position du chromosome une configuration possible du jeu. Chaque caractère définit le coup à exécuter dans la situation définie par la position du caractère. Considérons à titre d'exemple le cas n = 6. Le joueur A, qui commence, peut rencontrer 22 situations différentes. Représentons-en quelques-unes (voir fig. 3).
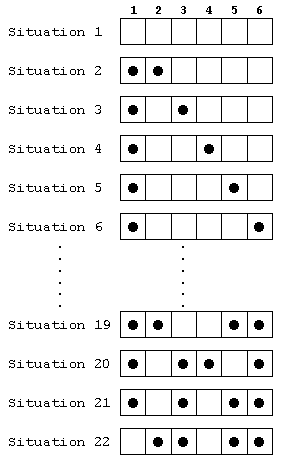
fig. 3. Quelques configurations que pourrait rencontrer le
joueur A lorsque n = 6.
La première situation à laquelle le joueur A peut
être confronté est un damier vide, les 15 suivantes sont
des damiers recouverts de 2 pions, les 6 suivantes sont des damiers
recouverts de 4 pions. Dans la situation 1, A peut choisir entre 6
actions: jouer en 1, en 2, en 3, en 4, en 5, ou en 6. Dans les situations
2 à 17, A a le choix entre 4 actions. Dans les situations 18
à 22, il ne lui reste chaque fois que deux possibilités.
Pour définir sans aucune ambiguïté la stratégie
d'un joueur qui commence, il suffit d'indiquer la manière dont
il jouerait dans chacune des 22 situations qu'il est susceptible de
rencontrer. Pour n = 6, le premier joueur a donc
le choix, sans tenir compte de la symétrie, entre 61 * 415 * 26 = 412'316'860'416
stratégies différentes.
Le joueur B peut lui aussi lors d'un partie rencontrer 22 situations
différentes (voir fig. 4). Les 6 premières situations
auxquelles B peut être confronté sont des damiers recouverts
d'un seul pion, les 16 autres sont des terrains recouverts de 3 pions.
Lorsqu'il n'y a qu'un pion sur le damier, B a le choix entre 5 actions;
lorsqu'il y en a 3, il a le choix entre 3 actions. Le joueur B a donc
à sa disposition 56 * 316 = 672'605'015'625
stratégies différentes.
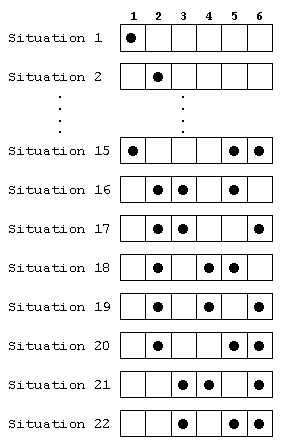
fig. 4. Quelques configurations que pourrait rencontrer le joueur
B lorsque n = 6.
Supposons que les stratégies des joueurs A et B soient définies par les deux chromosomes suivants (voir fig. 5):
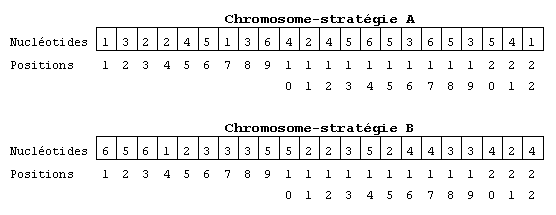
fig. 5. Exemples de génotypes.
Ces deux chromosomes représentent le génotype des joueurs
A et B. S'ils s'affrontent voici leurs échanges (voir fig. 6):
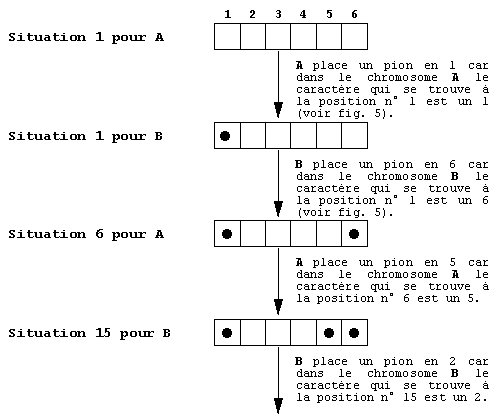
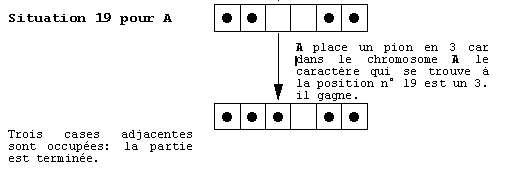
fig. 6. Une expression des génotypes définis dans
la figure 5.
Cette partie est l'expression de l'information portée
par leur génotype, elle représente ce que nous pourrions
nommer les phénotypes des joueurs A et B.
Constituons maintenant deux échantillons aléatoires: le
premier extrait des stratégies de A, le second de celles de B.
Puis examinons comment évoluent ces deux populations, le passage
d'une génération à la suivante s'effectuant par
l'exécution d'un cycle complet composé des trois opérateurs
génétiques préalablement définis. Nous suivrons
les changements apparaissant dans les deux populations en évaluant
régulièrement leur diversité respective. Cette
diversité globale se détermine en moyennant les diversités
locales. En une position donnée x la diversité
d(x) s'évalue par une entropie relative (3):
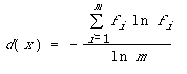
avec
- m: le nombre d'actions différentes qu'il est possible de choisir lorsqu'on se trouve dans la situation x;
- fi: la proportion des individus de la population optant dans la situation x pour l'action i.
La diversité locale, d(x), prend une valeur comprise
entre 0 et 1. Si d(x) = 0, alors la diversité
est nulle, tous les individus de la population choisissent dans la situation
x la même action. Si d(x) = 1,
alors la diversité est maximale, toutes les actions semblent
équivalentes, aucune n'est préférée; dans
ce cas, pour tout i: fi = 1/m (4).
L'évaluation de la diversité nous fournira quelques
indices de l'évolution des stratégies. En effet,
si la diversité au sein d'une population diminue, cela signifie
que certains individus ont réussi à s'imposer. Ils savent
donc sûrement mettre en oeuvre de judicieux stratagèmes
et toujours opter dans les situations délicates pour le bon coup.
La diminution de la diversité au sein d'un population signale
donc que la connaissance qu'ont les individus de leur environnement
a augmenté.
A titre d'illustration (5), voyons,
lorsque n = 6, comment évolue la diversité
des populations A et B, formées chacune de 200 individus (voir
fig. 7).
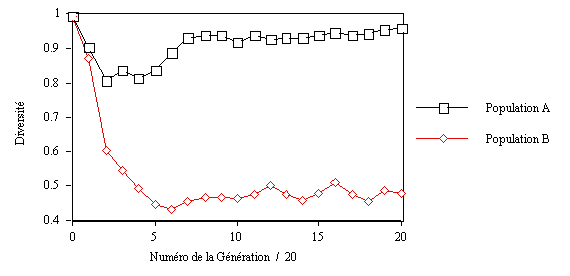
fig. 7. Évolution de la diversité au sein des populations
A et B, n = 6.
Au début la diversité est maximale dans les deux populations,
aucune force sélective ne s'est encore exercée sur elles.
Mais au cours du temps les deux populations se différencient
très nettement. La diversité de la population A commence
par diminuer légèrement, puis après quelques générations
se met à croître pour finalement atteindre la diversité
maximale. La diversité de la population B, quant à elle,
décroît de manière quasi-monotone pour converger
vers une valeur d'équilibre. En définitive seule la population
B change, se spécifie.
Sur le plan du jeu comment interpréter ces résultats ?
Remarquons que le jeu des triplets est un jeu à deux participants,
du type duel, dont les caractéristiques sont les suivantes: (1)
c'est un jeu "à découvert", c'est-à-dire
que chaque joueur connaît tous les éléments du jeu
à tout instant; (2) les deux joueurs jouent chacun à leur
tour; (3) aucun élément de hasard n'intervient au cours
du jeu; (4) le jeu se termine après un nombre fini de coups par
la victoire de l'un des deux joueurs (aucune partie nulle n'est possible)
(6). Dans ces conditions, en vertu
du théorème fondamental sur les jeux de combinaisons (7),
nous savons qu'il existe une stratégie gagnante pour l'un des
joueurs. Au jeu des triplets, lorsque n = 6, c'est
le joueur B qui possède cette stratégie. Ceci nous permet
de comprendre l'évolution des populations A et B. La population
A peut, lorsque les individus de B sont encore néophytes, exploiter
leurs erreurs et maladresses, sa variabilité diminue donc, jusqu'au
moment où une majorité des individus de la population
B découvrent une stratégie gagnante. Dès lors quoi
que fassent les individus de la population A ceux de la population B
gagnent. Alors que la pression adaptative s'exerce constamment sur la
population B, plus aucune force sélective n'agit sur la population
A qui va donc à nouveau se diversifier au maximum.
En puisant au coeur de la génétique, nous voulions proposer
un modèle mathématique qui puisse rendre compte de l'évolution
des stratégies d'un groupe d'élèves, c'est chose
faite ! A vous maintenant, cher lecteur, de juger à l'aune
de votre expérience la pertinence d'une telle proposition !
Post-scriptum: S'il est facile de montrer qu'au jeu des triplets
le premier joueur peut toujours gagner lorsque n est impair,
cela n'est plus aussi simple lorsque n est pair. Sur la plupart
des terrains pairs le joueur qui commence semble pouvoir gagner, mais
il y a des exceptions et celles-ci ne suivent aucune loi connue !
Bibliographie
CHAPEVILLE, F. ET AL. (1979). Le darwinisme aujourd'hui. Paris : Seuil.
DE POSSEL, R. (1936). Sur la théorie mathématique des jeux de hasard et de réflexion. In H. MOULIN, (1979), Fondation de la théorie des jeux (pp. 83-120). Paris : Hermann.
GARDNER, M. (1986). Le monde mathématique de Martin Gardner. Paris : Pour la science.
GENOUD, A. (1999). Les jeux de Nim. Math-Ecole, n° 186, 17-25.
HOLLAND, J. H. (1975). Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. Ann Arbor : The University of Michigan Press.
JAQUET, F. (1997). Jeux de NIM. Math-Ecole, n° 176, 25-34.
PIAGET, J. (1967). Intelligence et adaptation biologique. In Les processus d'adaptation: symposium de l'Association de psychologie scientifique de langue française, Marseille, 1965 (pp. 65-81). Paris : Presses Universitaires de France.
ZERMELO, E. (1913). Uber eine Anwendung der Mengenlehre auf die Theorie des Schachspiels. Proceedings, Fifth International Congress of Mathematicians, 2, 501-504.
(Cet article a également paru dans Math-Ecole no 187)