Introduction

Chaque civilisation, chaque région, voit se développer les mathématiques en liens étroits avec son contexte culturel, historique et social. Les cantons suisses, aux différents stades de leur confédération, ont aussi apporté leur pierre à l'édifice des mathématiques, dans le cadre élargi de l'Europe.

Cette exposé présentera quelques-unes de ces contributions, ainsi que leurs auteurs, dont on oublie souvent l'origine, dans le contexte historique, social et économique de la Suisse, dès 1291 jusqu'au XIXe siècle. De Joost Bürgi, à Ludwig Schläfli, en passant par d'autres mathématiciens que les Bernoulli, et Leonhard Euler, plusieurs mathématiciens d'origine helvétique ont leur place, à juste titre, dans l'histoire des mathématiques.

Le contexte Suisse de 1291 au XVIe siècle

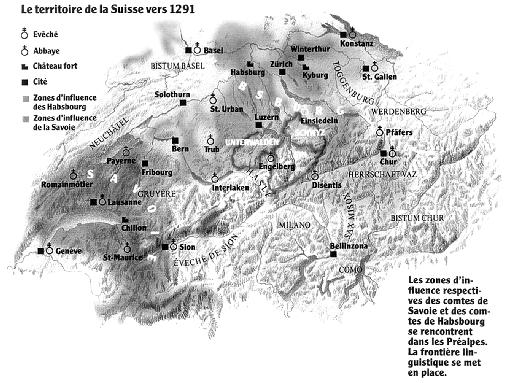
Le Moyen Age ne connaissait pas de territoires aussi nettement délimités qu'aujourd'hui.

Cette carte met en évidence les zones d'influence des comtes de Habsbourg, plus tard ducs d'Autriche, (au nord-est, en verte sur la carte) et des comtes de Savoie (au sud-ouest, en violet sur la carte) (2) .

Dans un Moyen Age plus mobile, plus créatif qu'on n'a longtemps voulu le croire, le XIIIe siècle, riche de vie et de mouvement, est un siècle de croissance, presque de révolution.

• Croissance démographique d'abord, la peste semblant en régression.
• Développement de l'agriculture: il faut donner du travail à de nouvelles forces et nourrir de nouvelles bouches.

Le commerce s'anime, les communications s'améliorant sur les grands chemins, les voies d'eau, les passages des Alpes.Les villes se développent ou se créent, centres d'une économie désormais à l'échelle régionale, villes portuaires ou se situant au passage des axes routiers, au franchissement des fleuves.

L' apparition des chiffres arabes, remplaçant la numération romaine dans les comptabilités, dés le milieu du siècle, contribue au développement des banques, du crédit. Les premières écoles sont créées dans les couvents et puis dans les 'Cités Médiévales'. Les écoles rattachées aux couvents étaient chargées d'instruire des clercs qui devaient assurer la relève.

le XIIIe siècle, notamment dans les cités, vit s'accroître chez les artisans et les marchants, la bourgeoisie de l'époque, le besoin d'acquérir une formation scolaire. Des écoles laïques sont fondées pour enseigner aussi le calcul.

Tablette de bois sculptée (Adelboden, BE, XVIe siècle) porte au recto et au verso l'alphabet latin, les chiffres arabes et romains.

L'artisanat, le commerce et le trafic avaient besoin d'une certaine mesure de paix et de sécurité. Deux voies s'offraient alors aux intéressés. Une cité qui sentait peser sur elle quelque menace povait se placer sous la protection d'un seigneur puissant; ainsi Berne et Genève, ville de foires, ont sollicité celle des comtes de Savoie; Zurich et temporairement Uri, celle des Habsbourg.

L'autre moyen de parer au danger était la formation d'une confédération régionale ayant pour objectif d'assurer la paix dans ses limites (3) . C'est ainsi que les trois cantons de Uri, de Schwyz et de Nidwalden, après la mort du roi Rodolphe Ier de Hasbourg (15 juillet 1291) conclurent, le 1er août déjà, un pacte pour se prémunir contre l'insécurité d'une double élection possible ou pour prévenir l'élection d'un roi étranger qui n'aurait pas été en mesure, comme Rodolphe l'avait fait, de s'occuper personnellement d'eux (4) .

Au cours du XIVe siècle les cantons confédérés arrivent à huit. Ils sont 13 en 1515, mais on compte aussi plusieurs "Pays alliés", selon divers statuts politiques et juridiques:

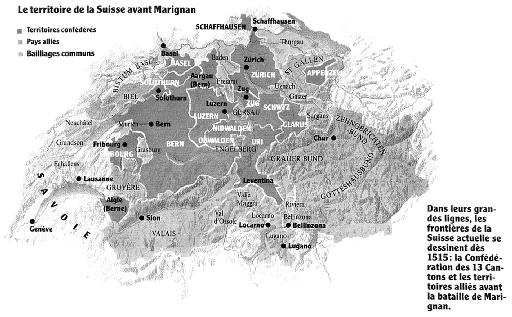
C'est bien dans un des pays alliés, la ville de Bâle, qu'on voit la fondation en 1460 de la première Université du territoire Suisse. L'Université de Bâle reste longtemps seule de son espèce en Suisse. Aux XVIe et XVIIe siècles, les villes ont installé des hautes écoles qui, contrairement aux universités, n'ont pas de statut d'autonomie. Les hautes écoles réformées et les collèges des jésuites occupent une place de choix dans l'organisation ecclésiastique des cantons. Jusqu'a la fin du XVIIe siècle, leur tâche a consisté surtout à enseigner la théologie et à former des prêtres et des pasteurs (5).

La Réforme entraîna la création d'“Ecole supérieures” dans toutes les grandes villes ayant embrassé le protestantisme : Zurich (1523), Berne (1528), Lausanne (1537), Genève (1595), Shaffhouse (1648) et enfin Saint-Gall (1713). En Suisse catholique, les gymnases jésuites reprirent l'enseignement secondaire général à Lucerne (1574), Fribourg (1580), Porrentruy (1591), Feldirch (dans le diocèse de Coire; 1649), Brigue (1662), Soleure (1668) et Sion (1734).

Donc la plupart des cités de la Confédération édifièrent bien leurs propres écoles mais les étudiants devaient aller acquerir leur diplôme universitaire à Bâle ou à l'etranger.

Les mathématiciens suisses du XVIIe siècle

C'est dans ce contexte qu'on retrouve la première contribution suisse importante au développement des mathématiques. C'est fut l'oeuvre de Joost Bürgi (1552-1632), originaire du Toggenbourg, horloger de la cour et astronome tout d'abord auprès du landgrave Guillaume IV de Hesse, puis auprès de l'empereur Rodolphe II à Prague et assistant du grand astronome Johannes Kepler (1571-1630)

C'est à Prague qu'il calcula une table d'antilogarithmes entre 1603 et 1611.
Il n'imprima ses “Progress Tabulen”, ses tables logarithmiques, qu'en 1620, bien des années après. Entre-temps, le mathématicien écossais John Napier (1550-1617) l'avait devancé en publiant en 1614 et 1619 son travail qui concerne le logarithme d'un sinus.

Si d'un côté le "droit d'aînesse" de Bürgi est bien établi par Kepler, Montucla (6) dit, d'une façon qui peut sembler d'une violence gratuite: “Remarquons toutefois que c'est à tort que de l'existence de cet ouvrage donné en 1620, on concluroit que Byrge auroit inventé les logarithmes antérieurement à Neper; car l'ouvrage de Neper avoit paru dès 1614, et c'est l'antériorité des dates des ouvrage, qui, au tribunal de l'opinion publique, décide l'antériorité de l'invention:”

Au delà de la priorité de publication, Bürgi et Neper travaillent indépendamment l'un de l'autre et les tables de logarithmes, qui répondaient pour les astronomes et les calculateurs à un besoin pressant, connurent un succès immédiat et considérable.

Saint-Gall, la ville de la toile de lin exporté dans toute l'Europe, donne naissance à Habakuk Guldin, qui, devenu jésuite, prendera le nom de Paul. On le present ici par les mots de Montucla : Le Père Guldin étoit né à St.-Gall, en 1577, et ayant ajuré le religion Protestant, il entra dans la compagnie de Jésus, en 1597, sous la semple qualité de Frère, ou de Coadjuteur temporel. Mais les talents qu'il montra pour les mathématiques, ayant frappé ses supérieurs, on l'envoya les cultiver à Rome, où il professa les mathématiques pendant quelques années.

Il les enseigna ensuite successivement à Gratz [ou il meurt en 1643] et à Vienne. La principale découverte qui rend l'ouvrage de Guldin (Centrobaryca ou de Centro gravitatis, 1635-1642) recomandable, consist dans l'application qu'il fait du centre de gravité à la mesure des figures produites par circonvolution.

“Toute figure - dit Guldin - formée par la rotation d'une ligne ou d'une surface autour d'un axe immobile, est le produit de la quantité génératrice par le chemin de son centre de gravité”.

Il n'est personne qui ignore que le cône droit est formé par un triangle rectangle, tournant autour d'un des côtés qui comprennent l'angle droit. L'on sait aussi que le centre de gravité de ce triangle est éloigné de cet axe du tiers de la base, et par conséquent il décrit une circonférence qui est le tiers de celle que décrit l'extrémité de cette base. La cône sera donc, selon Guldin, le produit du triangle générateur par le tiers de cette derniére circonférence, d'où l'on tire facilement, qu'il est le tiers du cylindre de même base et même hauteur (7).

Pendant son séjours en Italie Guldin rencontre Galileo Galilei (1564-1642), mais c'est avec un autre savant italien, Bonaventura Cavalieri (1598-1647), qu'il a une polémique assez violente. Dans son deuxième livre de la Centrobaryca (1640), Guldin attaque la théorie des indivisibles (8) de Cavalieri sur le plane de l'originalité et sur le plan de la rigueur.

Guldin affirme que les idées de Cavalieri viennent de Kepler et de Bartolemeo Souvey (voir plus loin). A son tour Cavalieri dit que Guldin aurait du nommé Pappus (vers 300) et ses Collectiones Mathematicae, a propos de son théorème sur la mesure des figures de l'espace.

Sur les questiones d'originalité, il faut une fois pour toutes mettre en clair que l'histoire des idées en général et l'histoire des mathématiques, en particulier, est pleine de disputes. Mais il faut aussi souligner que la théorie s'élabore à partir des idées de plusieurs personnes, retravaillée par chacune d'entre elles, améliorée et enfin formalisée.

Bartolomeo Souvey (connu comme Sovero), nommé auparavant, vient d'une famille de Corbière (Fribourg) et il est né vers l'année 1577. Il sera "Lecteur" de mathématiques à Padue à partir du mois de novembre 1624 jusqu'à sa mort en 1629. Sa seule oeuvre publiée, Curvi ac recti proportio, est sortie en 1630 en six livres dont le cinquième et le sixième sont les plus importants (9) . Il s'interesse ici entre autre des proprietés des courbes trascendantes.

Entre les XVIIe et XVIIIe siècles

Le mathématicien et astronome vaudois Nicolas Fatio (1664-1713) qui fut un collaborateur de Gian Domenico Cassini à Paris et plus tard de Newton en Angleterre, est représentatif d'un âge béni de la révolution scientifique où les savants pouvaient presque tout connaître et tout faire, où les grands esprits de L'Europe étaient en communication permanante, partageaient leurs résultats, se lançaient des défis et se posaient des problèmes les uns aux autres, enfin rivalisaient de rapidité pour apporter des solutions (Landes David, 1983). Emigré à Londres, il est élu à la Royal Society et il s'interesse entre autre à des problèmes mathématiques mis au concours. L'un de ces problèmes porte sur une question posée par Newton : Quelle est la forme de moindre résistance pour un solide ?: Fatio publie en 1701 une réponse élégante à cette question.(10)

Comme on le sait bien, la période à cheval des siècles XVIIe et XVIIIe est l'époque prestigieuse de la dynastie bâloise des Bernoulli qui se pencha sur le calcul infinitésimal, le calcul des probabilités, la théorie des nombres et la physique, en premier lieu Jakob Ier (1654-1705) et Johann Ier (1667-1748) dont le disciple Leonhard Euler (1707-1783) est le mathématicien le plus génial du XVIIIe siècle. De la mort de Fermat en 1665 à la naissance d'Euler en 1707, les conditions de la vie scientifique en Europe ont subi une considérable évolution.

Au temps des amateurs éclairés, échangeant entre eux une abondante correspondance, a peu à peu succédé celui des professionnels appointés, communiquant les résultats de leurs travaux dans des publications spécialisées. Euler fut à tous égards exceptionnelle: la publication de ses Oeuvres complètes, commencée en 1911 sous les auspices de la Société scientifique nationale helvétique n'est pas encore tout à fait achevée et a donné lieu à plus de 70 volumes (Guinot, 1994).

D'autres mathématiciens du XVIIIe siècle, d'influence culturelle française ou allemande, sont passer dans l'histoire: Johann Heinrich Lambert (1728-1777) de Mulhouse (ville qui à l'époque - à partir de la paix de Westphalie en 1648 et jusqu'au 1798 - était dans la Confédération Helvétique (11) ), Samuel König (1712-1757) de Berne (élève de Johann Bernoulli), Niklauss Fuss (1755-1826) de Bâle, représentèrent les sciences mathématiques au sein des Académies de Berlin et de Saint-Pétersbourg, Gabriel Cramer (1704-1752) et Jean-Louis Calandrin (1703-1758) oeuvrerent à Genève dans les domaines des mathématiques et de la philosophie.

On rappel ici quelques résultats au sein des mathématiques de Cramer et de Lambert.

Les concepts de déterminant et de matrice sont étroitement liés historiquement, tous proviennent de l'étude au cours du XVIIIe siècle des systèmes d'équations linéaires, que nous écrivons aujourd'hui:

xi = aij yj

où les xi sont connus et les yj inconnus.

Des 1678, Leibniz les avait abordés, et utilisé une notation à indices dans le cas d'un système de trois équation à deux inconnues. Il éliminait les deux inconnues et obtenait un déterminant dont la nullité était la condition de possibilité de résolution du système.

En 1748, Mac Laurin donne les formules de résolution explicites pour n = m = 2 et n = m = 3.

La méthode de résolution simultanée d'équations linéaires à plusieurs inconnues, sous forme de quotients de deux expressions, qui sont des polynômes multilinéaires par rapport aux coefficients du système, est explicitée par Cramer en 1754.

Lambert, Philosophe et Mathématicien, fut membre de l'académie de Berlin en 1765. Il a innové en préparant les géométrie non euclidiennes. Son nom est resté attaché en cartographie à une projection encore utilisée de nos jours. Son oeuvre de logicien à été trop peu étudiée.Lambert étudie la perspective, notamment dans son livre La Perspective affranchie de l'embarras du plan géométral, en 1759.

Dans sa préface, il indique comment simplifier les règle de construction perspectiviste en explicitant leurs principes.

Pour Lambert les règles ont à la fois une fonction pratique et une fonction théorique, celle-ci définie par l'effectivité de la méthode. En 1761, Lambert démontre que est irrationnel (en 1882, Lindemann établit la transcendance de ).

Lambert a 33 ans, en cette année 1761, où Rousseau publie la Nouvelle Héloïse, adresse à L'Académie des Sciences de Berlin un mémoire (qui ne sera lu qu'en 1767) intitulé "Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmetiques".

Ce mémoire est rédigé en français (Lambert qui a appris le français à quinze ans, écrit essentiallement en Allemand et pour une part en Latin). Sa structure est de forme assez classique pour le dixhuitième siècle.

Un exposé des motifs rédigé presque entièrement en langue commune, qui occupe deux pages et demie, et développe à la fois les intentions de l'auteur et l'état de la question et des idées à son époque, puis un corps de texte assez analogue aux textes modernes, c'est à dire un mélange bien particulier d'écriture et de signes symboliques mathématiques et la rhétorique qui les enchaîne, enfin, et dans les deux dernière pages, un retour à la pure rhétorique, dans un très pertinent exorde au style parfois prophétique.

Le XIXe siècle

Dans son Essai sur une matière de représenter les quantités imaginaires dans les constructions géométriques paru en 1806, Jean Robert Argand (Genève 1768 - Paris 1822) fournie une représentation géométrique des nombres complexes. Après les résultats de Gauss dans ce domaine, on parle du plan D'Argand-Gauss. Au sein de l'école allemande, le fossé se creuse rapidement entre les géomètres, qui privilégient la forme et veulent créer une géométrie purement descriptive, et les analystes, qui favorisent les méthode algébriques.

Les représentants les plus intransigeants de la première tendance sont Steiner et Staudt, tandis que Möbius et Plücker refusent de bannir les coordonnées de la géométrie projective.

Fils d'un agriculteur bernois, Jakob Steiner (1796-1863), élève de Pestalozzi à Yverdon, fut professeur de géométrie à l'Université de Berlin. L'oeuvre de Steiner s'inscrit dans le développement de la géométrie projective, après le travail de Poncelet, et consacre le renouveau de l'école mathématique allemand. Steiner devint un spécialiste de la géométrie dite “synthétique”, discipline dans laquelle ses ouvrages font encore autorité de nos jours.

C'est au Genevois Charles Sturm (1803-1885) que l'on doit des connaissances importantes en algèbre, en géométrie et en calcul différentiel. Professeur à l'Ecole Polytechnique, auteur d'un cours de mathématiques, Sturm était desservi par une écriture alambiquée. Son nom est resté attaché à un théoréme de nature algorithmique sur la recherche des racines réelles des équations algébrique.

Sa contribution essentielle est l'étude entreprise avec Liouville de certaines équations différentielles du second ordre avec des conditions aux limites. Il publie ses résultats principaux dans les travaux : “Mémoire sur la Résolution des équations numériques ” (1835) et “Mémoire sur les Lignes du second ordre” (1825-26).

Pour conclure cette aperçu historique sur la Suisse et ses mathématiciens je rappel ici encore Ludwig Schläfli (1814-1895) de Graswyll (Berne). Il fait ces études sécondaire auprés du Gymnase de Thun et ses études universitaires à l'Université de Berne ou, en 1863, il devient Professeur.

Il est un des créateurs de la géométrie pluridimensionnelle.

Schlafli is Alive and Well and Living in a Hollywood Studio


BIBLIOGRAPHIE
Dahan-Dalmedico, A:/Peiffer, J.: 1987, Une histoire des mathématiques, routes et dédales, Editions du Seuil.
Dhombres, J., & all.: 1987, Mathématiques au fil des âges, gauthier-villars Paris.
Guinot, M.: 1994, Ce diable d'homme d'Euler, Aléas Editeur.
Landes David, S.: Revolution time : Clocks and the Making of the Moderne World, 1983.
Montucla, J. F.: (AN VII), Histoire des Mathématiques, tome deuxième.
Serfati, M.: 1992, Quadrature du cercle, fractions continues et autres contes, Brochure A.P.M.E.P. n° 86.
Treichler, H. P.: 1991, L'aventure Suisse de siècle en siècle, Presse Migros.
Ulivi, E.:, 1990, Le quadratrici di Bartolomeo Sovero, L'educazione Matematica, Anno XI, Serie III, n. 2, 103-121.
La Suisse de la formation des Alpes à la quête du futur, 1975, 583-584.