4. QUELQUES EXEMPLES TIRES DES CLASSIQUES MATHEMATIQUES

4.1 Le théorème de Pythagore

C'est par la preuve de ce théorème qu'ouvre le plus ancien traité de mathématiques chinoises, le Zhoubi Suanjing Le classique du gnomon et des voies célestes circulaires. Voici comment il s'énonce: Si nous coupons un rectangle par sa diagonale, en prenant comme largeur 3 unités et comme longueur 4 unités, la longueur de la diagonale sera de 5 unités.

Le texte détaille ensuite comment on arrive à cette solution. Nous examinerons d'abord la première preuve que donne le texte lui-même, puis une autre proposée par un commentateur, le fameux Liu Hui.

Première preuve:

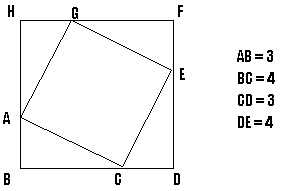
• 1. Soit un rectangle de côtés 3 et 4; traçons la diagonale;
• 2. élevons un carré sur cette diagonale;
• 3. ajoutons au carré ainsi obtenu trois nouveaux triangles, de sorte que le carré élevé sur la diagonale, l'hypoténuse (1), soit circonscrit par ce nouveau carré.

Fig. 6 Le théorème de Pythagore

La surface du carré BDFH est égale à (4 + 3) x (3 + 4) = 49;
la surface des quatre triangles est de (3x4)/2 x 4 = 24;
la surface du carré ACEG est donc de 49 - 24 = 25;
le côté, l'hypoténuse AC du triangle ABC est donc la racine de 25soit 5.

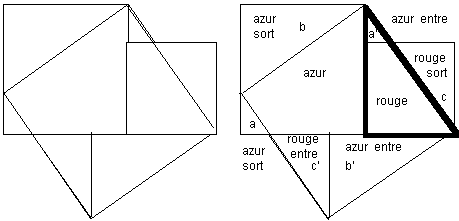
La deuxième preuve, celle de Liu Hui opère avec les notions intuitives de recoupement de triangles égaux et de déplacements, un peu comme un puzzle ou tangram chinois. Le raisonnement proprement dit repose sur un ingénieux travail de recoupement. Liu Hui cherche à montrer que les surfaces engendrées par le carré construit sur la base du triangle et par le carré construit sur le côté du triangle recouvrent sans restes la surface du carré construit sur l'hypoténuse.

Fig. 7 Le théorème de Pythagore d'après Liu Hui

Le triangle dont nous partons est celui dessiné en gras sur la figure de droite (2). Le petit carré était dessiné en rouge; le grand en azur.

4.2 Le calcul de

Le fait que rayon et circonférence d'un cercle sont d'un rapport constant est probablement une découverte déjà ancienne. Ce qui nous intéresse, pourtant, sont les tentatives faites pour calculer très exactement ce rapport ainsi que les méthodes utilisées pour arriver à cette fin. Il faut noter également que a toujours été conçu comme un rapport de grandeur en Chine. Le terme que les chinois utilisent pour décrire est justement zhoujing milü, ce qui veut dire " le rapport secret entre la circonférence et le diamètre ". Les Egyptiens et les Mésopotamiens avaient trouvé 25/8 = 3,125 < > sqrt(10) = 3,162.

Mais c'est probablement Archimède (287-212) qui a tenté le premier calcul théorique de . La méthode d'Archimède repose sur ce que l'on a appelé plus tard la quadrature du cercle (3). Comme le périmètre d'un polygone peut être calculé en connaissant le rayon du cercle dans lequel il est inscrit et le nombre de côtés, Archimède a tenté de calculer la circonférence en augmentant toujours le nombre des côtés du polygone. Le propre de la méthode d'Archimède a été de travailler avec un polygone inscrit et un polygone circonscrit (voir diagramme) et son résultat s'exprime donc sous forme de deux valeurs, assez rapprochées l'une de l'autre et entre lesquelles est compris. Archimède conclut ainsi que la valeur de est plus grande que 223/71 (3,1408 ) et plus petite que 22/7 (3,1428). Ptolémée (+150) arriva à la valeur de 3,1416. Le mathématicien chinois Chong Ji (430-501 AD) proposa la valeur de 355/113. Le mathématicien arabe Al'Khwarizmi (c. 800 ) n'eut pas mieux que 3,1416; mais Al'Kashi (c. 1430) calcula 14 places exactes derrière la virgule. Les Européens feront parler d'eux au 17e siècle seulement, avec Van Ceulen, qui calcula 17 places exactes. Il est intéressant de remarquer que le flambeau mathématique passe, pour un millénaire au moins, de l'Occident au monde oriental (chinois, indien et musulman). Il y eut donc beaucoup d'approximations de , mais seulement deux tentatives théoriques, celle d'Archimède et celle de Liu Hui (+260) et de son continuateur Zu Chongzhi (429-500). Tournons-nous donc vers la méthode de Liu Hui. Non satisfait de l'estimation de à 3, comme cela était écrit dans le Jiuzhang suanshu, Liu Hui songea à développer non pas une meilleure approximation, mais chercha à trouver une véritable méthode. Il ne s'éloigne pas très loin d'Archimède, mais son raisonnement est plus économique et ses résultats sont plus exacts. Comme Archimède, Liu Hui part également de polygones, mais seulement de polygones inscrits et il tente de calculer la longueur des côtés des polygones de plus en plus complexes. En fait il est allé au polygone de 192 côtés. Voici le raisonnement de Liu Hui:

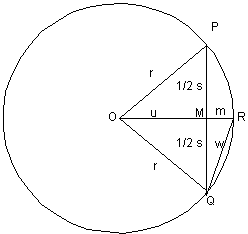
Il part, comme Archimède, d'un hexagone inscrit dans un cercle. Le périmètre d'un hexagone régulier inscrit dans un cercle peut être calculé; il vaut 3 fois le diamètre du cercle circonscrit; le côté de l'hexagone vaut donc le sixième de cette valeur. A partir de là, s'est dit Liu Hui, nous pouvons calculer le côté d'un polygone régulier qui soit le double de l'hexagone, donc d'un dodécagone (la valeur de w). Il prend appui deux fois sur le théorème de Pythagore pour trouver les valeurs, d'abord du triangle OMP, puis du triangle RMQ. Ainsi:

OM = u = sqrt(r² - (s/2)²)
MR = m = r - u
RQ = w = sqrt(m² - (s/2)²)

L'opération est ainsi répétée, jusqu'à 192 côtés. Liu Hui avait pris une valeur de 10 pour le rayon; le côté de son hexagone vaut ainsi également 10, en vertu du calcul (20x3)/6. Pour un polygone à 12 côtés, le calcul de se fait ainsi:

u = sqrt(100-25) = 8,660254037844
m = 10 - 8,660254037844 = 1,339745962156
w = 5,176380902051

Ensuite, il faut multiplier par 12, puisque c'est un dodécagone, et diviser par le diamètre, donc: (12x5.176380902051)/20 = 3,105828541231. Liu Hui a trouvé comme valeur (4) pour un polygone de 192 côtés = 3,141024.

Fig. 8 Le calcul de d'après Liu Hui

4.3 Le calcul par " fausse position "

Passons ensuite à une autre spécialité chinoise, à savoir le calcul dit par fausse position. En chinois, il s'appelle " technique du trop ou du pas assez " (ying bu zu shu). Il fait l'objet du chapitre 7 du Jiuzhang suanshu.

Voici un problème typique:

Fig. 9 Problème de fausse position

Un groupe de personnes achètent des poules. Si chaque personne avait donné 9 wen (unité de monnaie), on aurait pu acheter toutes les poules et garder en réserve une somme de 11 wen. Si, par contre, chaque personne avait donné seulement 6 wen, il aurait manqué 16 wen pour acheter toutes les poules. Combien y a-t-il de personnes dans ce groupe et quel est le prix du lot de poules?

Nous avons coutume, maintenant de donner des solutions algébriques; mais la solution offerte ici par le Jiuzhang suanshu est ingénieuse, et fait appel à nouveau aux fameuses baguettes de calcul.

1. Ecrire les contributions de chaque groupe sur la première ligne et l'excès ou défaut de chaque groupe sur la deuxième ligne.

9	6
11	16

2. Multiplier en croix (9x16; 6x11) et noter ce résultat sur la première ligne.

144	66
11	16

3. Additionner les deux produits.

210

27

4. Diviser le premier produit par la différence qu'il y avait entre les deux contributions (3 = 9-6). Le résultat donnera le prix total des poules (210/3 = 70). 5. Diviser également le deuxième produit par cette même différence. Le résultat donnera le nombre des acheteurs (27/3 = 9).

Voici encore un autre problème du même type, pris dans le même chapitre 7 du Jiuzhang suanshu. C'est la première fois que l'on rencontre des problèmes dit " de poursuite " dans l'histoire des mathématiques:

Fig. 10 Un problème de poursuite

Soit deux chevaux, un bon et un mauvais, qui quittent Chang'an pour se rendre à Qi. La distance entre Chang'an et Qi est de 3000 li. Le bon cheval avance de 193 li le premier jour et, les jours suivants, augmente son parcours de 13 li par jour. Le mauvais cheval avance de 97 li le premier jour et diminue ensuite son parcours d'un demi li par jour. Le bon cheval atteint Qi le premier puis revient sur ses pas et rencontre le mauvais cheval. Après combien de jours les deux chevaux se rencontrent-ils et quelle distance auront-ils alors respectivement parcourue?

Réponse: 15 jours et 135/191 jours; le bon cheval a parcouru 4534 li et 46/191 de li; le mauvais cheval 1465 li et 145/191 de li.

Procédé: supposons 15 jours. Le pas assez vaut alors 337 li et 1/2 de li (5). Supposons 16 jours. Le surplus vaut alors 140 li. Multiplions en croix les valeurs du trop et du pas assez, ajoutons [les résultats trouvés] et considérons [le total de ces deux valeurs] comme un dividende. En effectuant la division, on trouve le nombre de jours. " (6)

Les énigmatiques explications du Jiuzhang suanshu sont désormais claires pour nous, puisqu'il faut, dans ce problème de poursuites, procéder exactement comme auparavant. Mathématiciens, à vos baguettes!
1.

15	16
337,5	140

2.

2100	5400
337,5	140

3.

7500

477,5

4. Cette étape ne fait aucun changement, puisque la différence entre les deux valeurs supposées initiales est de 1. 5. Diviser. Le résultat est 15,70680628272 , ou exprimé en fractions 15000/955, c'est-à-dire 3000/191 ou 15 + 135/191.

La distance parcourue par les deux chevaux se calcule aisément ensuite.

5. LA DIFFUSION ET LA NATURE DU SAVOIR MATHEMATIQUE CHINOIS

Pour conclure, ne parlons pas seulement des mathématiques, mais aussi des mathématiciens en Chine. Nous avons appris que le système d'éducation de la Chine ancienne et médiévale était fort bien développé. Il est d'autant plus décevant d'apprendre que les mathématiciens étaient moins estimés que les lettrés en Chine médiévale. Pourtant, les premiers mathématiciens ont toujours été principalement des astronomes de cour, plus précisément des calendéristes, et jouissaient d'une grande considération. On était souvent aussi mathématicien de père en fils. Pendant la dynastie des Sui et des Tang (6e au 10e siècle de notre ère), les mathématiques de haut niveau étaient enseignées dans des Académies. Toutefois, " les étudiants en mathématiques étaient recrutés parmi les gens du peuple et les fonctionnaires du bas de la hiérarchie " (7). Les études étaient fort longues, 7 ans, et se basaient sur une collection et une anthologie de traités mathématiques, les fameux Dix classiques de calcul. Les examens avaient lieu une fois par an (8).

Les mathématiques occidentales furent introduites vers la fin du 16e siècle, comme nous l'avons déjà vu, mais ne mirent pas fin à la tradition chinoise autochtone.

Que devons-nous, Occidentaux créateurs de la science expérimentale et de la technologie scientifique, aux mathématiques chinoises? Les avis divergent profondément et la vérité est certainement à mi-chemin entre l'optimisme un peu démesuré de Joseph Needham et du scepticisme castrateur d'un Martzloff, spécialiste français contemporain des mathématiques chinoises. S'il est difficile de répondre au problème des influences et des priorités, fort complexe, puisqu'il y a eu flux et reflux des découvertes, une chose pourtant est sûre: la Chine ancienne et médiévale n'a eu besoin de personne pour arriver là où elle est arrivée, c'est-à-dire:

• avoir travaillé avec le système décimal (2e millénaire avant notre ère) et une préfiguration du zéro (4e siècle avant notre ère);
• avoir su extraire des racines carrées et cubiques;
• avoir découvert les nombres négatifs; -
• avoir découvert les fractions; - avoir prouvé le théorème de Pythagore; -
• avoir trouvé une méthode pour déterminer ;
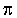• avoir posé et résolu des problèmes algébriques, à trois inconnues et plus; -
• avoir développé une technique algorithmique efficace.

La grande différence se situe plutôt au niveau des applications: le monde Occidental moderne s'est servi des mathématiques pour arracher à la nature des secrets de plus en plus nombreux; les mathématiques chinoises ont été, par contre, des mathématiques douces, conçues pour classer et trier ce qui était déjà là.

Pour en savoir plus

1. J. Needham, " Misères et succès de la tradition scientifique chinoise ", in: La science chinoise et l'Occident, Paris: Seuil, 1973
2. J. Needham, Science and civilisation in China. Vol. 3 Mathematics and the sciences of the Heavens and the earth, Cambridge, 1975
3. Histoire d'algorithmes : du caillou à la puce, par Jean-Luc Chabert et autres, Paris: Belin, 1994
4. J.-C. Martzloff, Histoire des mathématiques chinoises, Paris: Masson, 1988
5. G.G. Joseph, The crest of the peacock: non-European roots of mathematics, London ; New York: Tauris, 1991

Enfin, il y a un aperçu vraiment bien fait sur l'histoire des mathématiques sur le serveur WWW du Department of Mathematics and Computer Science de Clark University. L'adresse INTERNET est la suivante: http://aleph0.clarku.edu/