Cette liste de formules est extraite de le rubrique de Jean-Paul Delahaye (1999) Formules pour les nombres premiers. Pour la Science, 256, février.p. 100-105.

Dans ce qui suit le symbole [n] est à lire comme: partie entière de n.

Une formule "farce-et-attrape"

Il existe un nombre réel L tel que le n-ième nombre premier est donné par:

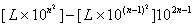
L'attrape est due au fait que L=0,200300005000000700000001100... (le n-ième nombre premier se trouve placé en position n²). Il faut juste se convaincre que dans cette construction, les nombres ne vont pas se chevaucher.

Formule de Yéléhada

Cette formule donne tous les nombres premiers, mais avec répétition et pas forcément dans l'ordre

Formules de Minác

C'est la "simplification de la formule de Yéléhada grâce au théorème de Wilson: (p-1)! + 1 est un multiple de p ssi p est premier:

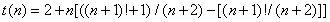
Formule de Minác et de Willans (1995)

Donne les nombres premiers dans l'ordre et sans répétition

Formule des nombres premiers jumeaux

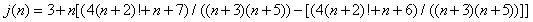
Cette formule engendre tous les nombres premiers jumeaux (mais on ignore si elle prend un nombre fini ou infini de valeurs différentes)

Formule de Willans (1964)

Elle donne le nombre de nombres premiers inférieurs à m:

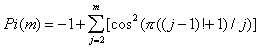
Formule de Hardy

Elle donne le plus grand facteur premier de N:

Formule de Polezzi (1997)

Elle donne le plus grand diviseur commun de n et m:

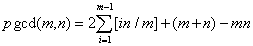
Formules donnant "beaucoup" de nombres premiers

n2 - n + 41	n = 0, ..., 40	Euler
103n2 - 3945n + 34381	n = 0, ..., 42	Ruby
47n2 - 1701n + 10181	n = 0, ..., 42	Fung
36n2 - 810n + 2753	n = 0, ..., 44	Ruby

Dans l'article de Pour la Science, le lecteur trouvera encore des information sur les polynômes de Matiiassevitch.