Société des enseignants
neuchâtelois de sciences(SENS)
BULLETIN No 20 / Théorie de l'information
Quelques aspects élémentaires de la théorie de l'information
L.-O. Pochon, IRDP
Dans le cadre d'un enseignement par situation-problèmes, on
trouve fréquemment utilisés les problèmes de minimum
de pesées ou le jeu des questions (trouver un élément
inconnu en posant un minimum de questions). Cas par cas, il est souvent
possible de se convaincre de l'aspect optimal des solutions trouvées
par bon sens, intuition et raisonnement ad hoc. Toutefois, il peut apparaître
des doutes sur la solution proposée. La théorie de l'information
fournit un cadre général à ce genre de problèmes
qui permet de lever certaines ambiguïtés.
Voulant me rafraîchir la mémoire à propos de
cette théorie, j'ai parcouru principalement les deux ouvrages très
classiques de Shannon (Shannon & Weawer, 1963) et de Yaglom (Yaglom
& Yaglom, 1969). J'en ai extrait les principaux résultats simples
et des exemples. Ce travail étant réalisé, il m'a
semblé qu'il pourrait être utile à d'autres collègues,
d'où cette brève note.
On notera que la théorie de l'information dans la lignée
du calcul des probabilités est fortement liée à des
situations que l'on pourrait qualifier "d'intuitives", se présentant
fréquemment dans la "vie courante". Certains principes
devront donc être acceptés qui concernent l'adéquation
du modèle à la réalité. Dans le cas des probabilités
la "Loi unique du hasard" (1)
de E. Borel représente l'un de ces principes. Mais cela peut nous
entraîner à utiliser les concepts en fonction de leur signification
"intuitive" et non selon leur définition ou leurs propriétés
mathématiques. Ecueil qu'il s'agit bien entendu d'éviter.
Notions de base
On considère une source d'événements aléatoires
Ai, i variant de 1 à k. peut aussi bien être une
source de messages, qu'une expérience dont les Ai sont
les résultats possibles, etc.
On notera pi = p(Ai) la probabilité de l'événement
Ai. On a évidemment 
pi = 1.
On définit l'entropie de la source comme étant la
quantité:
La fonction f(x) = x log x est définie sur l'intervalle ]0, 1]
et prolongée par continuité sur [0,1] (f(0) = 0).
H(
) est
un nombre toujours positif. Il peut être interprété
comme le degré d'incertitude concernant les résultats de
l'expérience. C'est aussi le potentiel de l'expérience à
apporter de l'information (2).
Le minimum de H()
est 0. Cette valeur n'est atteinte que s'il existe k tel que pk=1
et pi=0 
i
k (une seule
issue certaine!). Par ailleurs, on a le résultat suivant:
Ce fait se démontre en utilisant la convexité
de f(x) ou, en deux coups de cuillère à pot, à
l'aide des multiplicateurs de Lagrange.
L'unité utilisée est le "bit" si la base du
logarithme utilisé est, comme ici, 2. D'autres choix sont possibles
(3).
Un exemple est donné par une expérience à 2 issues,
auquel cas H()
log 2
= 1, l'égalité valant lorsque les deux issues sont équiprobables.
Si et
sont
deux expériences indépendantes (la sortie de Ai
n'ayant pas d'influence sur les p(Bj) et vice-versa, on
a:
|
Exemple 1 H( L'incertitude est alors inférieure. Les résultats
numériques correspondent bien à l'aspect intuitif
des notions en jeu. |
En général les sources ne sont pas indépendantes.
On définit alors l'entropie "conditionnelle": HAi()
= - pAi(Bj)
log pAi(Bj)
Dans cette expression pAi(Bj) représente
la probabilité conditionnelle p(Bj /Ai).
HAi()
est l'entropie de la source sachant que a
produit Ai
On peut alors définir l'entropie de sous condition de réalisation
de .
Avec cette définition, on a:
)
ne sont pas forcément toutes inférieures à H(),
on a:
H()
= 0 est équivalent à pAi(Bj) = 0 ou
1 i, j, ce qui justifie
dans ce cas de nullité de H(),
l'interprétation suivante: détermine
complètement .
(4)
Lorsque H()
= H(),et
sont dites
indépendantes.
Toutes ces formules se démontrent directement par des calculs simples
sur des logarithmes sauf (6) qui fait appel à quelques résultats
sur les fonctions convexes. On peut encore montrer par (5), (6) et un
par raisonnement par "récurrence" que:
avec le résultat intuitif que l'égalité
étant d'autant mieux réalisée que les i
sont indépendantes.
Par symétrie on a:
Lorsque
détermine complètement
(c'est-à-dire: H()
= 0), on a :
|
Exemple2
Ainsi la réalisation de l'expérience |
L'exemple précédent montre l'intérêt de définir l'apport de concernant l'incertitude de par l'information contenue dans
relative à :
H() est donc
aussi l'information totale de .
Depuis (8), tous les résultats proviennent de simples manipulations
de formules, ils augmentent les possibilités expressives de la
théorie sans ajouter de nouvelles propriétés (5).
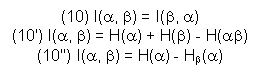
La relation 10''' nous dit également que l'information apportée
par
vaut son entropie si détermine
complètement (H()
= 0).
On a encore par 10'') et pour des raisons de symétrie:
L'information apportée par
à la détermination de
ne peut ni excéder l'information totale (l'incertitude) de
ni sa propre information totale.Le jeu des questions
Le problème suivant est bien connu:
| Exemple 3 Combien faut-il de questions pour deviner un nombre entier positif au plus égal à 1000 choisi en pensée par un interlocuteur. Les seules questions admises sont celles dont la réponse est oui ou non. |
Une première étape consiste à d'adapter le modèle théorique à cette situation réelle en faisant confiance à un principe d'adéquation.
La façon de procéder indiquée, par exemple par Yaglom, est la suivante: on considère l'expérience qui consiste à tirer un nombre parmi 1000. Chaque nombre a autant de chance d'être choisi et donc H(
)
= log 1000 = 9.97.On note
(k)
= 1
2 ...
k une suite de k questions (expériences) à deux
issues (réponse oui ou non). En principe on s'arrange pour que H()
= 0 mais ce n'est pas obligatoire pour la suite. Pour ces expériences
on a: H(
i)
log 2 et par
7) H((k))
k log 2 = k
Pour que
(k)
détermine entièrement ,
il faut que H(k)
() =
0 (on rappelle que cela signifie de fait une famille de probabilités
conditionnelles égales soit à 1 soit à 0). De (8) on
tire l'inégalité: log 1000 = H()
H((k))
k donc k >= 9.96 et donc k >= 10.Et on voit que cela est possible en 10 questions, en posant la question qui à chaque fois départage en deux les solutions et en rendant les questions indépendantes les unes des autres possibles ("est-ce ce que le nombre pensé est inférieur à 500?", etc.). Dans ce cas un raisonnement direct (ou le bon sens) en dit tout autant et l'apport de la théorie est, dans ce cas, limité.
On peut utiliser des interprétations plus parlantes en utilisant la définition de I(
(k),
) = H()
et en passant par elle pour l'inégalité: H()
= I((k),
) H((k))
k . Ce qui se
lit: l'information apportée à la détermination de par
(k),
doit être égale à l'incertitude de .
Cette information est inférieure à l'entropie de (k).Il faut toutefois noter qu'il n'est pas possible d'utiliser la théorie qu'à moitié et d'imposer directement que H(
(k))
doit être au moins égal à H()
arguant que l'information apportée par (k)
doit être supérieur à l'incertitude présentée
par . En effet,
nul ne nous assure que tous les raisonnements menés à l'aide
des signification attribuées vont forcément correspondre aux
propriétés formelles liées à la définition
de H. Un autre problème est déjà plus intéressant et la solution directe moins évidente:
| Exemple 4 Soient trois villes A, B et C telles que les habitants de A disent toujours la vérité, les habitants de B mentent toujours, tandis que les habitants de C donnent alternativement une réponse vraie et une réponse fausse. Un observateur veut déterminer dans quelle ville il se trouve et de quelle ville provient la personne qu'il a rencontrée. Combien de questions à réponse oui ou non faut-il ? |
Il y a 9 (= 3x3) issues à l'expérience de détermination de la ville et de l'origine de l'interlocuteur. Par conséquent le nombre k de questions doit satisfaire l'inégalité: log 9 <= k log 2 = k donc k est au moins égal à 4.
On trouve que 4 questions suffisent par exhibition des questions, par exemple:
1) Suis-je dans l'une des villes A ou B?
2) Suis-je dans C?
3) Habitez-vous la ville C?
4) Suis-je dans la ville A?
A partir de la réponse à la question 2) on peut savoir si l'interlocuteur provient de C ou non. La question 3) permet dans le premier cas de déterminer l'ordre de l'alternance entre vérité et mensonge et donc la ville où l'on se trouve. Dans le deuxième cas, elle permet de déceler la provenance de l'interlocuteur et si l'on se trouve dans C ou non. Dans ce dernier cas la question 4) permet de trancher entre les villes A et B. (6)
Le problème des pesées
Une autre famille d'énigmes est donnée par les problèmes des pesées sur une balance à deux plateaux sans l'utilisation de poids auxiliaires.
| Exemple 5 On a 25 pièces de monnaies d'apparence identique. Mais 24 d'entre-elles sont de même poids alors que l'une est un peu plus plus légère que les autres. La question est de savoir combien de pesées au minimum sont nécessaires pour désigner la pièce la plus légère. |
Dans ce cas l'expérience
a 25 issues et donc H()
= log 25. Une pesée donne une information au plus égale
à log 3. Donc log 25 <= H((k))
<= k log 3 = k et donc k >= (log 25)/log 3 = log3 25
et donc k >= 3.
On peut effectivement facilement montrer que 3 pesées sont suffisantes
en commençant par mettre 8 pièces sur chacun des deux plateaux.
Deux raisons peuvent conduire à cette solution. Tout d'abord, parce
que c'est elle qui rend la situation la plus symétrique et donc
l'arbre de recherche de hauteur minimale. Mais du point de vue de la théorie
de l'information, cette configuration est à préférer
parce qu'elle conduit à une distribution des probabilités
des 3 issues possibles (pencher à gauche, pencher à droite,
équilibre) la plus homogène et donc ayant l'entropie la
plus forte. Cette distribution des probabilités des réponses
peut être notée [1, 1, 1[ (probabilité de 1/3 pour
chaque issue de ).
Le cas suivant est un peu plus instructif dans ce sens:
| Exemple 6 La situation est presque la même que précédemment avec 12 pièces de même poids et 1 pièce de poids différent des autres (sans que l'on sache si elle est plus lourde ou plus légère). Il s'agit de trouver la pièce non conforme et dire si elle est plus légère ou plus lourde que les autres. |
Dans ce cas l'expérience a 26 (= 2 x 13) issues et donc H(
)
= log 26 = 4.700. Une pesée donne une information au plus égale
à log 3. Donc log 26 <= H((k))
<= k log 3 = k et donc k >= (log 26)/log 3 = log3 26 et
donc à nouveau k >= 3.Mais dans ce cas on va démontrer que k ne peut pas être égal à 3 en montrant que la deuxième pesée apporte une information trop faible.
A nouveau, il est assez facile de voir (2 stratégies) que la première pesée la plus efficace est de mettre 4 pièces sur chaque plateau de la balance. La distribution des probabilités des issues est donnée par [4, 4, 5] et H(
1)
= 1.577 est très proche de log 3 (1.584). Pour la deuxième
pesée on s'intéresse au cas le plus défavorable,
c'est-à-dire celui où la pièce différente
est parmi les 5 qui n'ont pas fait partie de la première pesée
(cas d'équilibre) (7)
. On peut passer en revue le nombre de ces pièces que l'on
va mettre sur la balance (plateau de gauche, par exmple). Ce nombre peut
varier de 1 à 5. Les différentes répartitions des
probabilités (penche à gauche, à droite, équilibre)
sont les suivantes: [1, 1, 8] [3, 3, 6] [2, 2, 6] [1, 1, 8] [1, 1, 0]
auxquelles correspondent les valeurs de l'entropie suivantes: 0.922, 1.414,
1.252, 0.922, 1. La plus forte est 1.414. Ajoutée à celle
de la première expérience on a donc au maximum pour information
après deux pesées: 2.991 bits. Reste donc au moins une incertitude
de 1.71 bits, valeur supérieure à log 3. Une troisième
pesée ne pourra donc pas toujours suffire (8).
Cet examen nous indique également quelle est la deuxième
pesée à effectuer. La solution effective en 4 pesées est laissée au lecteur, de même que la solution en 3 pesées dans le cas où le nombre total de pièces est de 12 seulement (11 "normales" et 1 défectueuse).
Cette théorie ne donne qu'une borne inférieure au nombre d'expériences à effectuer. Par contre, le calcul de H peut fournir des heurisitques locales et ne saurait donner une marche à suivre globale. A noter que dans les exemples 3, 4 et 5, le simple dénombrement des réponses suffisait à calculer une borne inférieure raisonnable (équiprobabilité des réponses). L'exemple 6 montre déjà une plus grande complexité. Le cas du "Master mind" offre un autre exemple où la première approximation est trop grossière et où le calcul de la probabilité des réponses (qui peut dépendre de l'issue de ) peut s'avérer délicat.
Le cas du "Master mind"
| Exemple 7 On considère le jeu bien connu du "Master mind" dans un cas simple, avec 3 positions et des fiches de 4 couleurs (0, 1, 2, 3). Un code caché est constitué de trois fiches. Une question consiste à proposer une solution. Pour chaque proposition on répond par le nombre de fiches bien placées et parmi les fiches restantes celles de la bonne couleur. Par exemple, si le code à trouver est 012, la question 000 provoque la réponse (1,0). La question 131 donne lieu à la réponse (0,1). |
L'expérience
a 64 issues, donc H()
= log 64 = 6. Par ailleurs, il y a 9 réponses possibles à une question
(9).
On peut donc estimer H()
<= log 9 = 3.16, d'où k >= 6/log 9 >= 1.89 et donc k >=
2.Mais les probabilités des réponses sont très disparates. On peut en tenir compte pour une meilleure estimation de k (et aussi pour imaginer la suite des questions à poser).
Dans le tableau ci-dessous on présente la distribution des 9 réponses aux trois types de questions possibles. On voit que la meilleure question est la question 1.3 et que l'information apportée dans ce cas est nettement plus faible que la valeur 3.16 obtenue en supposant les réponses équiprobables. La nouvelle minoration de k est donc 3.
Réponse |
Question 1.1: 000 |
Question 1.2: 001 |
Question 1.3: 012 |
(3,0) |
1 |
1 |
1 |
(2,0) |
9 |
9 |
9 |
(1,2) |
- (10) |
2 |
3 |
(1,1) |
- |
8 |
12 |
(1,0) |
27 |
17 |
12 |
(0,3) |
- |
- |
2 |
(0,2) |
- |
5 |
15 |
(0,1) |
- |
14 |
9 |
(0,0) |
27 |
8 |
1 |
H |
1.54 |
2.67 |
2.74 |
On se contente ici d'étudier la question suivante dans le cas le plus "défavorable" (la question 012 a provoqué la réponse (0,2)):
Dans ce cas 15 codes sont encore possibles: 100 101 103 121 123 130 200 203 220 221 230 231 301 320 321. La distribution des réponses est la suivante pour des questions de trois types différents:
Réponse |
Question 2.1: 210 |
Question 2.2: 013 |
Question 2.3: 123 |
(3,0) |
- |
0 |
1 |
(2,0) |
3 |
0 |
2 |
(1,2) |
0 |
1 |
1 |
(1,1) |
6 |
2 |
4 |
(1,0) |
0 |
0 |
3 |
(0,3) |
0 |
2 |
1 |
(0,2) |
6 |
6 |
2 |
(0,1) |
0 |
4 |
1 |
(0,0) |
0 |
0 |
0 |
H |
1.52 |
2.07 |
2.79 |
La question 2.3 est la meilleure. Dans le cas le plus "défavorable"
(réponse (1,1)) les codes possibles sont: 130 203 221 320 et
la question 320 permet de trouver le bon code (dans ce cas H=2). Trois
questions suffisent et peuvent s'avérer nécessaires (11).
Quelques remarques concernant ce dernier exemple permettront de conclure
sur les apports et les limites de cette théorie dans le cas de
la résolution de ce type de problèmes.
Tout d'abord il est clair que le calcul de l'entropie n'est pas chose
aisée. Il ne semble pas y avoir ici de possibilité de
la calculer sans passer par la recherche des distributions des réponses
(merci l'ordinateur). Par ailleurs, la question optimale n'est pas toujours
nécessaire (dans ce cas la question 1.2 suffit également
pour trouver le code en trois questions) et est même à
éviter s'il s'agit de travailler mentalement (12).
Dans les algorithmes utilisés communément sur ordinateur
(Messulan, 1978), on choisit également la question 1.3 mais pour
une autre raison. En effet, c'est aussi avec cette question que le plus
faible maximum dans la fréquence des réponses est enregistré.
Mais il peut arriver que ces deux stratégies conduisent à
des choix différents (la distribution [8, 8, 8, 1] a pour entropie,
1.764 alors que l'entropie de [9, 5, 5, 6] est plus élevée
avec une valeur de 1.954). Cette observation permet de rappeler l'aspect
statistique de la définition de H. Utiliser cette théorie
ne conduit pas forcément trouver un optimum "hic et nunc",
mais de tabler sur une stratégie la plus efficace dans la durée
lors de la répétition de l'expérience.
En définitive, la théorie de l'information peut être
abordée simplement, elle met en œuvre la fonction logarithme
et le calcul des probabilités et permet de réfléchir
au lien entre mathématique et réalité. Mais, elle
n'évite pas de se "salir les mains" dans les exemples
pratiques.
A noter encore que ce formalisme est utilisé, entre autres, dans
la théorie du codage, la théorie de la mesure, l'interprétation
des "tests d'hypothèse" sans compter les parallélismes
à faire avec l'entropie définie en thermodynamique.
Références
Escarpit, R. (1976). Théorie générale de l'information
et de la communication. Paris: Hachette.
Messulan. J. (1978). Jouons au "Master mind" avec un ordinateur. Pentamino, 5, 57-63.
Shannon, C. E. & Weawer, W. (1963). The mathematical theory of communication. Urbana: University of Illinois Press.
Yaglom, A. M. & Yaglom, I.M. (1969). Probabilité et information. Paris: Dunod.
Watanabe, S. (1969) Knowing & Guessing. New York:
John Wiley & Sons.