Société des enseignants
neuchâtelois de sciences (SENS)
BULLETIN No 19 / Mathématiques
A vieux théorème démonstration nouvelle
André Calame, Chemin de Fresens 15, CH-2026 Sauges
Il arrive parfois qu'un mathématicien publie une démonstration inédite d'un théorème bien connu depuis plusieurs siècles. Ceci est particulièrement intéressant quand la nouvelle démonstration repose sur des notions récentes que l'auteur de la démonstration initiale ne pouvait pas utiliser. En voici un exemple:
| Tout nombre premier de la forme p = 4k + 1 est décomposable en une somme de deux carrés. |
Quelques illustrations:
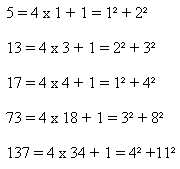
Ce théorème, cité par Fermat a été
démontré par Euler au milieu du 18ème siècle.
Sa démonstration porte sur l'existence d'une décomposition;
elle ne donne pas un procédé de calcul qui permettrait de
construire effectivement la décomposition.
Les démonstrations classiques de ce théorème se réfèrent à d'autres résultats de la théorie des nombres : petit théorème de Fermat théorème de Wilson, restes quadratiques, etc. La plupart des démonstrations sont indirectes ou par l'absurde : supposer que p n'est pas la somme de deux carrés conduit à une contradiction.
Or, une démonstration nouvelle, dans un contexte tout différent, a paru en 1990 sous la plume de D. Zagier. Cette démonstration est directe et elle repose essentiellement sur la notion d'involution; de plus, elle ne fait appel à aucun résultat antérieur.
Rappelons qu'une involution définie sur un ensemble E est une bijection F autre que l'identité, qui coïncide avec la bijection réciproque.
(En géométrie, toutes les symétries du plan et de l'espace sont des involutions.)
Etant donné une involution F définie sur E,
- il se peut qu'un élément coïncide avec son image:
F(a) = a
On dit alors que a est un élément fixe ou invariant. Ce n'est certainement pas le cas de tous les éléments de E, sinon F serait l'identité, ce qui est exclu par définition.
Si F(a) = a' et a' a, alors on a F(a') = F [F(a)] = a
Les éléments de E qui ne sont pas fixes se correspondent
par paires.
Exemple : E = {2, 3, 4, 5, 7, 10, 13, 19, 37}, ensemble des diviseurs
de 36, augmentés de 1
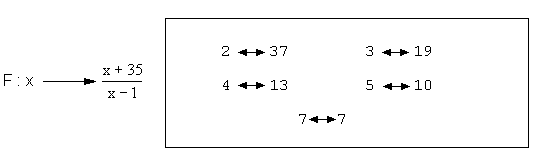
En généralisant cet exemple, on a les deux propriétés
suivantes :
PROPRIETE A : Si une involution définie sur un ensemble fini a un seul élément fixe, le nombre des éléments de E est impair.
PROPRIETE B : Si le nombre des éléments de E est impair, toute involution définie sur E admet au moins un élément fixe.
Avant d'aborder la démonstration de Zagier, commençons
par une remarque. Comme p = 4k + 1 est un nombre impair, sa décomposition
en somme de deux carrés comprend un carré impair, disons
x2, et un carré pair, disons 4y²; d'où la
relation :
Zagier généralise cette équation en x et y et envisage toutes les solutions de l'équation
dans l'ensemble des nombres naturels. Chaque solution est un triplet (x,y,z)
et nous noterons E(p) l'ensemble des triplets solutions.
A titre d'exemple, voici les 11 solutions de l'équation (1) pour
p = 41 = 4 x 10 + 1, k=10:
x |
y |
z |
1 |
1 |
10 |
1 |
2 |
5 |
1 |
5 |
2 |
1 |
10 |
1 |
3 |
1 |
8 |
3 |
2 |
4 |
3 |
4 |
2 |
3 |
8 |
1 |
5 |
1 |
4 |
5 |
2 |
2 |
5 |
4 |
1 |
L'avant-dernière ligne fournit la décomposition de p = 41 en somme de deux carrés:
Le plan de la démonstration de Zagier a l'avantage de s'exprimer très aisément à l'aide des deux propriétés des involutions rappelées plus haut.
- Le nombre des solutions de l'équation (1) dans E(p) est toujours un nombre impair. On le prouve en construisant sur E(p) une involution F avec un seul triplet fixe (propriété A).
- Comme E(p) a un nombre impair d'éléments, toute involution définie sur E(p) admet au moins un triplet fixe (propriété B).
- En particulier, l'involution qui conserve x et qui échange
y et z admet au moins un triplet fixe
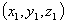 :
: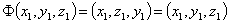 d'où
d'où 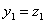 et
et 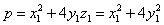
Cette dernière égalité est la décomposition cherchée.
On le voit, s'il y a une difficulté dans cette démonstration,
elle réside uniquement dans la construction de l'involution F du
point 1. Nous allons en donner une reconstitution en plusieurs étapes.
Même si cela nécessite quelques calculs, elle reste élémentaire
dans son esprit.
Première étape
Quel que soit p = 4k + 1 premier, le triplet (1,1,k) est solution de
l'équation (1):
1² + 4 x 1 x k = 4k + 1 = p
Déterminons une application linéaire F1 sur E de la forme
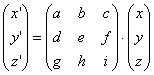
qui conserve le triplet (1,1,k), quel que soit k.
On doit avoir:
d + e + kf = 1
g + h + ki = k
d'où:
e = 1 - d f = 0
h = - g i = 1
si on veut des valeurs indépendantes de k. La matrice F1 devient:
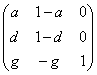
et on a:
y' = dx + (1-d)y
z ' = gx - gy + z
Deuxième étape
Le triplet (x',y',z') doit satisfaire comme le triplet (x,y,z) a la relation
(1):
[ax + (1-a)y]² + 4 [dx + (1-d)y] [gx - gy + z] = x² + 4yz
Les termes en yz doivent être égaux; d'où: d = 0
Les termes en x² doivent s'annuler; d'où: a²=1
De même, les termes en xy s'annulent; d'où:
Si a = 1, on a g = 0 et la matrice est la matrice unité, ce qui
est exclu.
Reste le cas a = -1 qui implique g = 1. La matrice cherchée est
alors
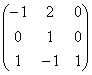
et on vérifie qu'elle est involutive. On a donc:
| F1: | x' = -x + 2y |
| y' = y | |
| z' = x - y + z |
Notre recherche est-elle terminée ? F1 est bien
une involution qui conserve le triplet (1,1,k) qui est le seul triplet
fixe, car:
x' = x implique x = y ;
la relation x² + 4yz = p devient x² + 4xz = p
donc : x(x + 4z) = p
et comme p est premier, on a nécessairement x = y = 1,
puis 1.(1 + 4z) = p = 1 + 4k et donc z = k
Dans l'exemple de p = 41, on voit que F1 échange (1,2,5)
et (3,2,4) d'une part, (3,4,2) et (5,4,1) d'autre part. Mais, l 'image
de (1,10,1) serait (19,10,-8) qui n'est pas un triplet de E(41). De manière
générale, F1 n'est définie que sur les
triplets de E(p) tels que
et z' = x - y + z >0 ou x > y-z
Autrement dit, il faut que x satisfasse à la double inégalité
Dès que p > 5, les triplets de E(p) se répartissent en
trois catégories:
a) les triplets qui satisfont les inégalités (2) et pour
lesquels l'involution F1 s'applique;
b) les triplets (x,y,z) tels que x > y-z dont (1,k,1) est un exemple;
c) les triplets (x,y,z) tels que x >2y dont ,(3,1,k-2) est un exemple.
Troisième étape
Nous devons donc compléter F1 par une autre application linéaire. Par analogie avec ce qui précède, on construit F2 qui transforme le triplet (1,k,1) de catégorie b) en (3,1,k-2) de catégorie c). On trouve:
| F2: | x' = x + 2z |
| y' = z | |
| z' = -x +y -z |
En passant, notons que F2 assure que les catégories b) et c) ont toujours le même nombre de triplets. F2 n'est pas une involution, mais on y remédie au moyen de F3, application linéaire réciproque de F2
| F3: | x' = x - 2y |
| y' = x - y + z | |
| z' = y |
Nous disposons enfin de l'involution cherchée F, définie en trois "morceaux" suivant les catégories a), b), c).
| F: | (-x+2y , y , x-y+z) si y-z < x < 2y |
| (x,y,z) (x+2z , z , -x+y-z) si x < y-z | |
| (x-2y , x-y+z , y) si x > 2y |
C'est sous cette forme condensée que D. Zagier a exprimé l'involution, sans donner de détails sur sa construction.
Pour terminer, nous illustrons F dans le cas p = 41, k = 10
x |
y |
z |
y-z |
2y |
Catégorie de (x,y,z) |
x' |
y' |
z' |
|
1) |
1 |
1 |
10 |
-9 |
2 |
a |
1 |
1 |
10 |
2) |
1 |
2 |
5 |
-3 |
4 |
a |
3 |
2 |
4 |
3) |
1 |
5 |
2 |
3 |
10 |
b |
5 |
2 |
2 |
4) |
1 |
10 |
1 |
9 |
20 |
b |
3 |
1 |
8 |
5) |
3 |
1 |
8 |
-7 |
2 |
c |
1 |
10 |
1 |
6) |
3 |
2 |
4 |
-2 |
4 |
a |
1 |
2 |
5 |
7) |
3 |
4 |
2 |
2 |
8 |
a |
5 |
4 |
1 |
8) |
3 |
8 |
1 |
7 |
16 |
b |
5 |
1 |
4 |
9) |
5 |
1 |
4 |
-3 |
2 |
c |
3 |
8 |
1 |
10) |
5 |
2 |
2 |
0 |
4 |
c |
1 |
5 |
2 |
11) |
5 |
4 |
1 |
3 |
8 |
a |
3 |
4 |
2 |
Référence: D. ZAGIER - A One-Sentence Proof That Every Prime p 1 (mod 4) Is a Sum of Two Squares - Amer.Math. Monthly, Vol.97, no.2 (February 1990), p.144.