INTRODUCTION

Quelques explications, d'abord, sur le titre (1) énigmatique: il ne s'agira pas d'explorer les zones d'ombres qui persistent dans les mathématiques chinoises - il ne s'agit pas davantage du nombre dans le théâtre d'ombres chinois. Les ombres dont nous parlerons sont celles que la culture chinoise ancienne et médiévale ne cesse de projeter sur la nôtre. Les sciences et les techniques chinoises ont, en effet, éclipsé pendant un bon millénaire (du 4e au 14e siècle de notre ère) les performances occidentales dans ce domaine.

Si l'on essaie de faire le bilan de ce que l'Occident doit à la civilisation chinoise, on pense d'emblée, bien entendu, aux trois grandes inventions que sont l'imprimerie, la poudre et la boussole (2). La recherche de ces cinquante dernières années - principalement celle de Joseph Needham et de son équipe à Cambridge - a montré que cette liste est probablement beaucoup plus longue, et comporte plusieurs éléments tout à fait inattendus. Inattendus dans la mesure où beaucoup de découvertes chinoises ont contribué à façonner l'aspect de notre réalité sociale, institutionnelle et technique au-delà de tout ce que l'on a pu imaginer jusqu'à maintenant.

Jusqu'au quinzième siècle de notre ère, la supériorité technologique et scientifique de la Chine sur le monde occidental a été évidente, même si nous - et les Chinois aussi - ne le savions pas. Le Moyen Age occidental n'aurait pu qu'admirer le haut niveau de la médecine et de la phytothérapie chinoises, auxquelles nous nous intéressons de plus en plus. Dans le même ordre d'idées, il faut encore mentionner l'alchimie, qui a permis aux Chinois la découverte de la porcelaine. De même, l'agronomie et la pédologie, ou la connaissance des sols, ont été beaucoup mieux développés qu'en Occident. N'oublions pas, bien entendu, la sériciculture, la culture de la soie, importante également par les connaissances qui ont transité par la fameuse route de la soie (3).

Joseph Needham a aussi montré que la Chine a légué à l'Occident d'autres découvertes capitales: celle de l'échappement en horlogerie (4), par exemple. Le principe de l'échappement, en effet, était connu en Chine dès le VIIIe siècle de notre ère. C'est vers la fin du XIe siècle que nous trouvons les premiers mécanismes d'horlogerie à échappement en Chine. Mais les horloges, en Chine, ne jouent un rôle qu'en astronomie. Le principe de l'échappement - dont le prototype chinois a été de type hydraulique - a ensuite été transféré en Occident, et aboutit, après plusieurs siècles de gestation, à la notion d'horloge individuelle, ou de montre. En Europe, il fallait ainsi attendre le XVIIe et le XVIIIe siècle pour rattraper et dépasser les Chinois, et permettre à nos Bovet de Chine d'importer leurs fameuses paires de montres.

Et, soit dit en passant, la Chine a également inventé un autre instrument, sans lequel la Suisse ne serait pas tout à fait ce qu'elle est - l'arbalète.

C'est encore de la Chine que vient le harnais efficace - celui qui tire sur l'épaule de l'animal - et qui remplace alors avantageusement le harnais à sangle de l'Occident médiéval. L'étrier est également une découverte chinoise, de même que la courroie de transmission, la manivelle, le bateau à roue à aubes, la brouette et ... les spaghettis.

Ensuite, si nous quittons le domaine artisanal, nous pouvons noter que la bureaucratie est également une invention chinoise. Ses principes sont énoncés dès le quatrième siècle avant notre ère; les critères du recrutement et du contrôle des fonctionnaires sont déjà clairement établis. La notion de portefeuille, de contrôle administratif, de fonction sont acquises. C'est encore à la Chine que nous devons le système des examens, qui servaient précisément à recruter des fonctionnaires et non à traumatiser de jeunes âmes sensibles. Toute personne se destinant à une carrière officielle, en effet, devait passer par les examens impériaux, et les aspirants s'y préparaient pendant plusieurs années.

C'est également en Chine ancienne (4e siècle avant notre ère) que nous assistons au développement des premières universités - ou Académies. Ces vastes cités du savoir, qui abritaient plusieurs centaines voire milliers d'érudits étaient censées réfléchir aux meilleurs moyens pour gouverner le pays, mais toute participation active à la vie politique leur avait été sagement interdite. Nous y trouvons aussi, pour la première fois dans l'histoire de l'humanité, ce qu'on a pris coutume d'appeler la médecine légale (5).

Une telle énumération de hauts faits techniques et culturels étonne, et la question qui se pose est évidemment celle-ci: " ... pourquoi la science moderne, comme mathématisation d'hypothèses relatives à la nature, avec toutes ses implications dans le domaine de la technologie avancée, fait-elle une ascension rapide seulement en Occident, à l'époque de Galilée? " (6).

A cette question fait pendant une autre question: " pourquoi, entre le IIe siècle avant notre ère et le XVIe de notre ère, la culture de l'Est asiatique a-t-elle appliqué avec beaucoup plus d'efficacité que l'Occident européen la connaissance humaine de la nature à des fins utiles? " (7).

Mais on peut poser également une troisième question, plus profonde et plus embarrassante: " comment cela se fait-il qu'une grande civilisation comme celle de la Chine n'a pas été bouleversée comme celle de l'Occident par la découverte et la possession d'une telle quantité d'instruments de domination et de destruction? ".

La réponse à ces questions ne pourra naître que d'une étude minutieuse des conditions sociales, économiques et politiques ayant prévalu à l'Est et à l'Ouest, étude à peine commencée. Toujours est-il que les découvertes scientifiques et techniques chinoises se sont déversées, comme J. Needham se plaît à nous le rappeler, dans le grand océan de la science oecuménique et notre culture scientifique contemporaine aurait certainement pris une toute autre forme si elle n'avait pas reçu l'apport de l'Orient, non seulement chinois, mais également indien et musulman.

Nous commençons à nous apercevoir aujourd'hui, beaucoup mieux qu'auparavant, du cheminement du savoir depuis l'Antiquité. L'opinion traditionnelle, qui veut que notre patrie scientifique se trouve en Grèce, et que son savoir nous ait été transmis à travers le monde arabe sans en avoir bénéficié beaucoup, est intenable aujourd'hui (8).

Il est non moins évident que toutes ces découvertes et inventions de la Chine ancienne et médiévale auraient difficilement pu être mises en valeur sur un arrière-fond mathématique médiocre. Et on peut dire sans hésitation que la Chine a aussi été, comme toutes les autres grandes civilisations, une civilisation du nombre. Plusieurs raisons peuvent nous l'expliquer:

1. En premier lieu, il faut mentionner l'astronomie. Les Chinois calculaient les solstices depuis l'Antiquité; ils étaient passés maître dans la science du calendrier;
2. une deuxième source aura pu être, comme en Egypte, l'arpentage;
3. en troisième lieu, les Chinois ont depuis toujours appliqué la statistique, pièce maîtresse de la gestion administrative et bureaucratique mises en place dès le milieu du -4e s.;
4. la Chine a possédé de tout temps de brillants ingénieurs et artisans, qui avaient l'habitude d'entreprendre de grands travaux publics: endiguement, canalisation, construction de ponts. De telles activités sont inimaginables sans le secours des mathématiques.

Malgré toutes ces conditions favorables, nous ne trouvons pas en Chine l'idée de la mathématisation de l'univers, c'est-à-dire la croyance inconditionnelle que tous les aspects de la réalité sont structurés par les nombres et contrôlables par eux. Cet aspect est typique de l'esprit grec ainsi que de la Renaissance occidentale et est à la base du devenir de la science et de la technique modernes. La Chine n'a donc jamais été, comme les Grecs, opposée au choc de la découverte de grandeurs mathématiques irrationnelles, comme par exemple .

En Chine prévaut certes également une idée très forte de la régularité des phénomènes cosmiques; mais cette régularité est patente, ouverte; on en est convaincu d'avance, et on ne se sent pas obligé de la démontrer. Il ne faut pas des expériences et des hypothèses pour contraindre cette régularité à s'exhiber. Dans sa deuxième préface (1787) à la Critique de la raison pure, le philosophe allemand Immanuel Kant a très bien décrit l'essence de la méthode expérimentale propre à l'Occident. Il l'explique à peu près en ces termes: la raison doit se comporter face à la nature non pas comme un élève face au maître, mais comme un juge face à des témoins, un juge qui " force les témoins à répondre aux questions qu'il leur pose ". Voilà une attitude que l'on ne trouve pas du tout en Chine ancienne et médiévale. Le savant chinois n'est pas quelqu'un qui cherche à arracher des secrets à la nature.

On chercherait également en vain un quelconque exotisme dans les mathématiques chinoises. Les mathématiques chinoises sont résolument tournées vers des applications, et ce n'est pas un hasard si le record de décimales exactes pour ¹ a été tenu par les Chinois pendant un millénaire et demi. " Dans les manuels mathématiques médiévaux européens, les problèmes étaient, pour l'essentiel, imaginaires, tandis qu'en Chine ils provenaient de situations de la vie de tous les jours. " (9) . Nous en verrons plusieurs exemples par la suite.

Il faut insister, cependant, que l'histoire des mathématiques en Chine, même si elle est connue dans ses grandes lignes, reste à explorer pour les détails. La production a été immense: les spécialistes estiment à un millier le nombre de traités mathématiques écrits en Chine, sans compter les commentaires.

Les mathématiques occidentales arrivent en Chine vers la fin du 16e siècle, par l'intermédiaire des jésuites. Elles auront un impact assez grand à cette époque, mais pour une raison très particulière. Les Chinois sont émerveillés surtout par la science du calendrier occidentale, le seul domaine où ils pouvaient, à ce moment, vraiment apprendre quelque chose des Occidentaux. Les jésuites étaient loin de l'ignorer, et ils comptaient là-dessus pour faire avaler aux Chinois la pilule du christianisme qu'ils savaient amère. L'entreprise, comme nous le savons aujourd'hui grâce aux nombreuses lettres des premiers missionnaires jésuites, n'allait pas dans le sens prévu par les autorités ecclésiastiques, et quelques-uns des meilleurs jésuites étaient bientôt plus influencés par les Chinois que leur foi ne pouvait le tolérer!

Or la supériorité occidentale dans la science du calendrier ne reposait pas sur l'appareil mathématique, mais plutôt sur le modèle astronomique sous-jacent. L'univers chinois, en effet, a toujours été conçu comme géocentrique, avec une terre plate; l'accent a toujours été mis sur l'observation (10), jamais sur la modélisation hardie de la mécanique céleste en cercles et ellipses.

Après ce panorama introductif, tournons-nous à présent vers les mathématiques proprement dites, et commençons par le début, à savoir le système de numération.

1. LE SYSTEME DE NUMERATION

Le système de numération chinois remonte à la seconde partie du deuxième millénaire avant notre ère. Il est donc tout aussi ancien que l'écriture chinoise elle-même. Les plus anciennes traces que nous possédons de ce système sont celles que l'on trouve sur les os et les écailles de tortue, de la dynastie des Shang (1600 à 1066 avant notre ère). Ces écailles de tortue étaient utilisées à des fins divinatoires. Avant toute entreprise importante, le prince avait coutume de consulter l'oracle. Pour ce faire on perçait un ou plusieurs trous dans une écaille de tortue, et on la mettait dans le feu. Les craquelures qui s'y produisaient étaient alors interprétées par des devins. Ces parties de carapaces de tortue, découvertes à la fin du siècle passé seulement, étaient d'une importance capitale, puisque la question posée à l'oracle, ainsi que la réponse donnée, étaient gravées sur ce matériau. Ces écailles de tortue, que l'on a ensuite trouvées par dizaines de milliers, sont non seulement des documents culturels, mais également linguistiques de la plus haute importance. Le système de numération utilisé sur ces écailles et os de tortue est déjà remarquablement constant et unifié. Il utilise un total de treize signes:

Fig. 1 Le système de numération chinois




Notez en passant que le Chinois ne connaît pas de signe particulier pour marquer le million. Un million se dit simplement 100 x 10.000 (baiwan); dix millions se dit alors 1000 x 10.000, ce qui fait le désespoir des traducteurs. Plus tard, un signe particulier pour noter la valeur de 100 millions (yi) fut introduit. Le système standard d'écriture des nombres s'est stabilisé vers 200 avant notre ère déjà et n'a plus changé depuis.
Comparé à celui des autres vieilles civilisations, le système de numération des Chinois est en avance, grâce à sa simplicité et à sa systématicité. C'est un système décimal, qui de plus avait saisi l'importance du zéro, marqué simplement par un espace vide, et non encore par un symbole le dénotant expressément. Les premiers mathématiciens chinois, cependant, se sont servis, dès le milieu du premier millénaire avant notre ère, d'un autre système, parent - donc également décimal - mais adapté spécifiquement au maniement scientifique des nombres.

Cette notation à usage des mathématiciens utilise seulement 9 symboles - les chiffres de 1 à 9 - et représente également le zéro par l'absence ou la place vide. Les chiffres cependant sont représentés par des bâtons ou des baguettes posés horizontalement ou verticalement. On commence par se donner deux manières graphiquement distinctes, mais symétriques d'écrire les chiffres de 1 à 9. Voici les deux séries:

Fig. 2 Le système de numération mathématique chinois

Ce système de numération est basé sur deux principes :

1. la position et le rang des chiffres ;
2. l'alternance

Les valeurs de base qui seront notées sont les suivantes: - les unités (vertical) - les dizaines (horizontal) - les centaines (vertical) - les milliers (horizontal) - les dizaines de milliers (vertical)

Les symboles de la première série (les verticaux) sont donc utilisés pour noter les unités, les centaines, et les dix mille; les symboles de la deuxième série (les horizontaux) sont utilisés pour noter les dizaines et les milliers. Les deux séries se combinent ainsi, par simple alternance, dans l'écriture des nombres. Pour écrire 8947, on écrit, en commençant depuis la droite 7 vertical (unité), puis 4 horizontal (dizaine), puis 9 vertical (centaine), puis 8 horizontal (millier), en alternant donc toujours les horizontaux et les verticaux. Pour écrire 8907, on écrit, en commençant depuis la droite 7 vertical (unité), puis on laisse un espace vide pour marquer l'absence des dizaines, puis on écrit 9 vertical (centaine) et enfin 8 horizontal (millier).

Fig. 3 Exemples de numération chinoise

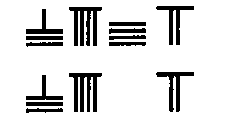
Il n'y a donc pas encore, en Chine ancienne, de symbole pour le zéro. Néanmoins, le zéro se traduit dans ce système par une place vide, et, également, par une anomalie dans le système d'alternance, dans le sens que deux séries identiques (deux horizontales ou deux verticales) se suivent.

Il n'est pas besoin d'insister, je crois, sur l'importance de la relation entre le progrès mathématique et le système de numération. La Chine antique y était presque arrivée; un millénaire avant que le symbole pour le zéro naisse en Inde vers le 8e s. de notre ère. Le système de numération chinoise laisse la place du zéro vacante, et cette place vide, ce trou dans l'écriture, fait directement référence aux calculs sur une grille virtuelle, appelée également " surface à compter " et cela nous amène à notre deuxième point, les méthodes de calcul.