Un tambour est constitué par une membrane vibrante fixée le long de son bord. En battant du tambour, on observe certaines fréquences, toujours les mêmes. Une modélisation du phénomène consiste à identifier le bord du tambour à une courbe simple fermée G du plan, et la membrane au repos avec le domaine D intérieur à G. Si le tambour résonne selon une fréquence w, l'amplitude des vibrations de la membrane dans la direction transverse est donnée par une fonction f(x,y) (dépendant du point (x,y) de D), qui vérifie l'équation aux dérivées partielles

 

et la condition f = 0 sur G, correspondant au fait que la membrane est fixée au bord. Ici c est une constante dépendant des propriétés physiques de la membrane, et de la tension avec laquelle on l'a tendue sur G.

Le problème mathématique sous-jacent s'appelle le problème de Dirichlet pour l'opérateur laplacien . En posant

,le problème est de trouver les nombres positifs l pour lesquels il existe une fonction f non nulle sur D telle que

(2) et f=0 sur G.

 

Un tel nombre l s'appelle une valeur propre de D; les fonctions non nulles qui sont solutions de (2) s'appellent fonctions propres, ou modes normaux ; elles correspondent aux amplitudes des ondes stationnaires émises par le tambour.

L'ensemble des valeurs propres est le spectre de D. En 1894, le Français Henri Poincaré a montré que le spectre est une suite qui tend vers l'infini: 0 <= l1 <= l2 <= l3 <= ... On a longuement étudié comment la géométrie du tambour influe sur les propriétés de la suite des (ln). En 1966, l'Américain Mark Kac pose le problème inverse : supposons que l'on connaisse la suite des (ln); cela nous permet-il de reconstruire la courbe G? De manière plus imagée: si nous pouvions écouter le tambour avec une oreille parfaite, et ainsi entendre toutes ses fréquences, pourrions-nous retrouver la forme du tambour? "Can one hear the shape of a drum?"(1)

La question de Kac se basait sur le fait que, dès 1912, l'Allemand Hermann Weyl avait montré que la connaissance du spectre de D permettait de retrouver l'aire de D et le périmètre de G; on savait aussi que deux tambours en forme de parallélogramme ont même spectre uniquement si les parallélogrammes sont isométriques. Ce n'est qu'en juin 1991 que les Américains Carolyn Gordon, David Webb et Scott Wolpert ont montré que, comme Kac le pressentait lui-même, la réponse à la question ci-dessus est négative: les deux tambours ci-dessous ont même spectre, mais n'ont clairement pas même forme. (2)

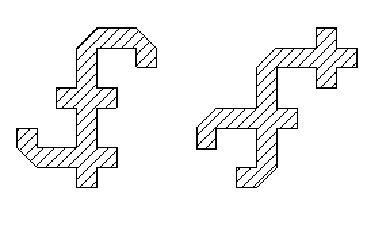
Ces deux tambours peuvent paraître tarabiscotés; ils sont cependant assez simples, puisque ce sont des contours polygonaux dont les arêtes sont de longueur 1, 2 ou , et dont les angles intérieurs valent 90°, 135° ou 270°. La preuve du fait qu'ils ont même spectre est un fascinant mélange d'analyse, de géométrie, et de théorie des groupes: l'interaction entre différents sujets se révèle souvent fructueuse en mathématiques.

(1) Ce "problème inverse" est très semblable à la démarche de la spectroscopie (noter à ce propos la similitude de terminologie): en spectroscopie, on cherche à identifier un corps en étudiant la lumière qu'il émet.

(2) On pourra vérifier que ces deux tambours ont même aire et même périmètre.